Iterated function system
A family  of mappings, where
of mappings, where 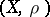 is a complete metric space. Usually,
is a complete metric space. Usually, 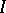 is a finite set,
is a finite set, 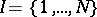 . An iterated function system is called hyperbolic if all
. An iterated function system is called hyperbolic if all  are contracting (cf. Contraction) for
are contracting (cf. Contraction) for 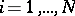 . An iterated function system induces a mapping
. An iterated function system induces a mapping 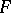 from the space
from the space 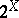 to itself by
to itself by 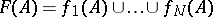 . If the iterated function system is hyperbolic and one restricts
. If the iterated function system is hyperbolic and one restricts  to the space of non-empty closed bounded sets equipped with the Hausdorff metric, then it follows from the contracting-mapping principle that
to the space of non-empty closed bounded sets equipped with the Hausdorff metric, then it follows from the contracting-mapping principle that 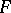 has a unique fixed point
has a unique fixed point  ; moreover,
; moreover, 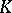 is compact ([a8], [a7]). The set
is compact ([a8], [a7]). The set 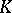 is called the attractor, or invariant set, of the iterated function system. If
is called the attractor, or invariant set, of the iterated function system. If 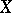 is a Euclidean space and the
is a Euclidean space and the  are similitudes, then the attractor is called a self-similar set. These sets are usually fractals (cf. Fractals); an example is the triadic Cantor set (cf. also Cantor set), which is the attractor of the iterated function system
are similitudes, then the attractor is called a self-similar set. These sets are usually fractals (cf. Fractals); an example is the triadic Cantor set (cf. also Cantor set), which is the attractor of the iterated function system
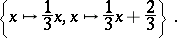 |
A generalization is the concept of a recurrent self-similar (or mixed self-similar) set generated by a recurrent iterated function system. Let 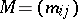 be an
be an 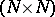 -matrix of zeros and ones satisfying
-matrix of zeros and ones satisfying 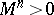 for some
for some  , and let contracting mappings
, and let contracting mappings 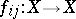 be given for each
be given for each 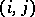 such that
such that 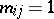 . Then (see [a3] or [a1]) there is a unique vector
. Then (see [a3] or [a1]) there is a unique vector 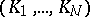 of non-empty compact sets such that for
of non-empty compact sets such that for 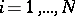 ,
,
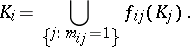 |
An iterated function system with probabilities is an iterated function system  together with a probability vector
together with a probability vector 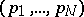 (i.e.,
(i.e., 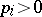 and
and  ). This induces a mapping
). This induces a mapping 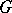 on the space of Borel probability measures by
on the space of Borel probability measures by 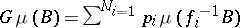 for all Borel sets (cf. also Borel set)
for all Borel sets (cf. also Borel set) 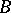 . If the iterated function system is hyperbolic, then there is a unique fixed point
. If the iterated function system is hyperbolic, then there is a unique fixed point  for
for 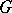 , i.e. an invariant measure, whose topological support is the attractor of the iterated function system [a7]. Convergence to
, i.e. an invariant measure, whose topological support is the attractor of the iterated function system [a7]. Convergence to  is also obtained by associating a random dynamical system with the iterated function system via the Markov chain
is also obtained by associating a random dynamical system with the iterated function system via the Markov chain  , where the
, where the  form a sequence of independent random variables with distributions
form a sequence of independent random variables with distributions 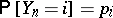 [a2]. The same type of result holds for recurrent iterated function systems, taking for
[a2]. The same type of result holds for recurrent iterated function systems, taking for 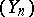 a Markov chain on
a Markov chain on 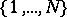 whose transition probabilities are positive if and only if the
whose transition probabilities are positive if and only if the 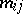 are positive [a3], [a4]. Iterated function systems are applied for approximation purposes (see, e.g., [a5]) and the construction of wavelets (see, e.g., [a6]).
are positive [a3], [a4]. Iterated function systems are applied for approximation purposes (see, e.g., [a5]) and the construction of wavelets (see, e.g., [a6]).
References
| [a1] | C. Bandt, "Self similar sets I. Topological Markov chains and mixed self-similar sets" Math. Nachr. , 142 (1989) pp. 107–123 |
| [a2] | M.F. Barnsley, D. Demko, "Iterated function systems and the global construction of fractals" Proc. Roy. Soc. London A , 399 (1985) pp. 243–275 |
| [a3] | M.F. Barnsley, J.H. Elton, D.P. Hardin, "Recurrent iterated function systems" Constr. Approx. , 5 (1989) pp. 3–31 |
| [a4] | J. Elton, "An ergodic theorem for iterated maps" Ergodic Th. & Dynamical Systems , 7 (1987) pp. 481–488 |
| [a5] | B. Forte, E.R. Vrscay, "Solving the inverse problem for measures using iterated function systems: a new approach" Adv. Appl. Probab. , 27 (1995) pp. 800–820 |
| [a6] | J.S. Geronimo, D.P. Hardin, P.R. Massopust, "Fractal functions and wavelet expansions based on several scaling functions" J. Approx. Th. , 78 (1994) pp. 373–401 |
| [a7] | J.E. Hutchinson, "Fractals and self-similarity" Indiana Univ. Math. J. , 30 (1981) pp. 713–747 |
| [a8] | R.F. Williams, "Composition of contractions" Bol. Soc. Brasil. Mat. , 2 (1971) pp. 55–59 |
Iterated function system. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Iterated_function_system&oldid=47448