Invariant metric

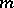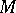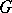A Riemannian metric on a manifold that does not change under any of the transformations of a given Lie group of transformations. The group itself is called a group of motions (isometries) of the metric 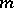(or of the Riemannian space ).

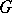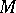A Lie group of transformations of a manifold acting properly on (that is, the mapping 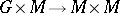, 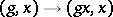is proper) has an invariant metric. Conversely, the group of all motions of any Riemannian metric (as well as any closed subgroup of it) is a proper Lie group of transformations. In this case the stabilizer (or isotropy group)

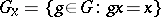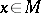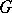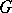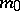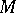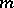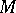of any point is a compact subgroup of . If itself is compact, then a -invariant metric can be constructed on by averaging any metric on over :

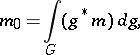where the integral is taken with respect to the Haar measure.

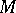If is transitive, can be identified with the space of cosets 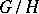of 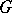with respect to the stabilizer 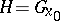of a fixed point 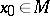, and in order that there exist a 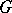-invariant metric on 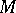it is necessary and sufficient that the linear isotropy group (see Isotropy representation) has compact closure in 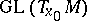(in particular, it is sufficient that 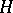be compact). 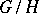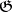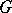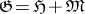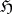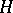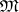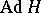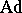In this case the space is reductive, that is, the Lie algebra of admits a decomposition , where is the subalgebra corresponding to and is a subspace that is invariant under where is the adjoint representation of (cf. Adjoint representation of a Lie group). If 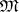is identified with 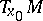, then any 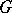-invariant metric 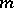on is obtained from some 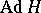-invariant Euclidean metric 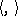on 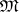in the following way:

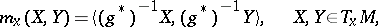where 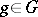is such that .

The tensor fields associated with a -invariant metric (the curvature tensor, its covariant derivatives, etc.) are 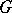-invariant fields. In the case of a homogeneous space 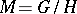, their value at a point 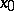can be expressed in terms of the Nomizu operator , which is defined by the formula

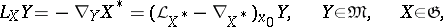where 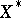is the velocity field of the one-parameter group of transformations 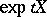, is the covariant differentiation operator of the Riemannian connection and 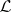is the Lie derivative operator. In particular, the curvature operator 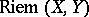and the sectional curvature 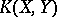in the direction given by the orthonormal basis 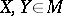satisfy the following formulas:

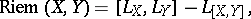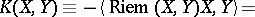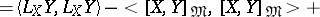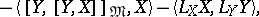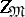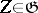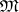where is the projection of on along .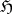

The Nomizu operators can be expressed in terms of the Lie algebra 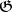and the metric 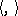by the formula

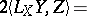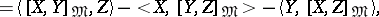where 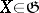, 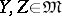. It follows from the definition of the Nomizu operators that their action on -invariant fields differs only in sign from that of the covariant derivative at the point 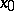. If the Riemannian space 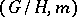does not contain flat factors in the de Rham decomposition, then the linear Lie algebra generated by the Nomizu operators 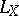, , 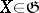is the same as the holonomy algebra (cf. Holonomy group) of the space 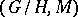at .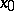

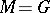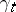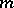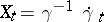A description of the geodesics of an invariant metric on a homogeneous space can be given in the following way. Suppose, to begin with, that is a Lie group acting on itself by left translations. Let be a left-invariant geodesic of the metric on the Lie group and let be the curve in the Lie algebra 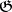corresponding to it (the velocity hodograph). The curve 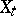satisfies the hodograph equation

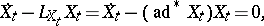where 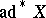is the operator dual to the adjoint representation 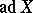. The geodesic 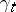can be recovered in terms of its velocity hodograph 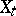from the differential equation 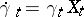(which is linear if the group 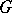is linear) or from the functional relations

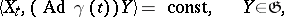giving the first integrals of this equation. Thus, the description of the geodesics of the metric 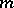reduces to the integration of the hodograph equation, which sometimes can be completely integrated. For example, in the case when the metric 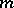is also invariant with respect to right translations, the geodesics passing through the point are the one-parameter subgroups of 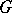. Such a metric exists on any compact Lie group. In the case of an arbitrary homogeneous space 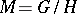an invariant metric 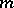on 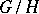can be "lifted" to a left-invariant metric 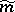on 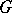for which the natural bundle 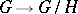of the Riemannian space 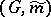over the Riemannian space 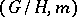is a Riemannian bundle, that is, the length of tangent vectors orthogonal to the fibre remains unaltered under projection. For this it is sufficient to extend the metric 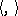to the entire algebra 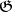by setting

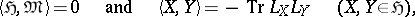and carrying it over by left translations to a metric 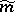on . The geodesics of are projections of geodesics of 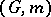that are orthogonal to the fibres.

Since the functi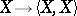on on 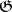is always a first integral of the hodograph equation (the energy integral), the corresponding equation of the vector field on 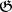is tangent to the spheres 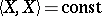. This implies the completeness of the hodograph equation and therefore also the completeness of any invariant Riemannian metric on a homogeneous space. For a pseudo-Riemannian metric the completeness property does not hold, in general. On the other hand, any invariant pseudo-Riemannian metric on a compact homogeneous space is complete.

See also Symmetric space.

References

[1]	S. Helgason, "Differential geometry, Lie groups, and symmetric spaces" , Acad. Press (1978)
[2]	A.Z. Petrov, "New methods in general relativity theory" , Moscow (1966) (In Russian)
[3]	S. Kobayashi, K. Nomizu, "Foundations of differential geometry" , 2 , Interscience (1969)
[4]	S. Kobayashi, "Transformation groups in differential geometry" , Springer (1972)
[5]	J.A. Wolf, "Spaces of constant curvature" , Publish or Perish (1984)
[6]	A. Lichnerowicz, "Geometry of groups of transformations" , Noordhoff (1977) (Translated from French)
[7]	A.L. Besse, "Einstein manifolds" , Springer (1987)

Comments

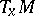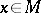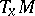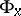A de Rham decomposition (of the tangent space at a point ) is defined as follows. Let , let be the tangent space at and let be the holonomy group of the Riemannian connection at . The group 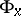acts on 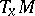. Let 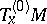be the subspace of tangent vectors that are left invariant under . Let 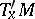be the orthogonal complement of 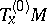in 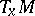and let 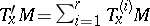be a decomposition of into mutually-orthogonal invariant irreducible subspaces. The decomposition

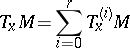is called a de Rham decomposition or a canonical decomposition.

An irreducible Riemannian manifold is one for which the holonomy group 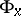acts irreducibly on 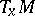(so that there is only one factor in the Rham decomposition of ).

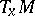The de Rham decomposition theorem says that a connected simply-connected complete Riemannian manifold is isometric to a direct product 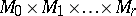where 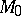is a Euclidean space (possibly of dimension zero) and where the 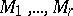are all simply-connected complete irreducible Riemannian manifolds. Such a decomposition is unique up to the order of the factors, [a1], Sect. IV. 6.

References

[a1]	S. Kobayashi, K. Nomizu, "Foundations of differential geometry" , 1 , Interscience (1963)