Invariant metric
A Riemannian metric 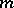 on a manifold
on a manifold 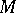 that does not change under any of the transformations of a given Lie group
that does not change under any of the transformations of a given Lie group  of transformations. The group
of transformations. The group 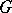 itself is called a group of motions (isometries) of the metric
itself is called a group of motions (isometries) of the metric 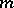 (or of the Riemannian space
(or of the Riemannian space  ).
).
A Lie group 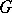 of transformations of a manifold
of transformations of a manifold  acting properly on
acting properly on 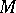 (that is, the mapping
(that is, the mapping 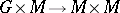 ,
, 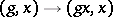 is proper) has an invariant metric. Conversely, the group of all motions of any Riemannian metric (as well as any closed subgroup of it) is a proper Lie group of transformations. In this case the stabilizer (or isotropy group)
is proper) has an invariant metric. Conversely, the group of all motions of any Riemannian metric (as well as any closed subgroup of it) is a proper Lie group of transformations. In this case the stabilizer (or isotropy group)
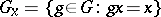 |
of any point 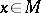 is a compact subgroup of
is a compact subgroup of 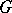 . If
. If  itself is compact, then a
itself is compact, then a 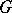 -invariant metric
-invariant metric 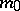 can be constructed on
can be constructed on 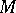 by averaging any metric
by averaging any metric 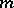 on
on 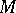 over
over  :
:
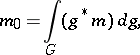 |
where the integral is taken with respect to the Haar measure.
If  is transitive,
is transitive, 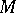 can be identified with the space of cosets
can be identified with the space of cosets 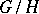 of
of 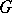 with respect to the stabilizer
with respect to the stabilizer 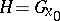 of a fixed point
of a fixed point 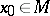 , and in order that there exist a
, and in order that there exist a 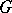 -invariant metric on
-invariant metric on 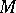 it is necessary and sufficient that the linear isotropy group (see Isotropy representation) has compact closure in
it is necessary and sufficient that the linear isotropy group (see Isotropy representation) has compact closure in 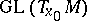 (in particular, it is sufficient that
(in particular, it is sufficient that 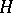 be compact). In this case the space
be compact). In this case the space 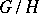 is reductive, that is, the Lie algebra
is reductive, that is, the Lie algebra 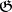 of
of 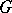 admits a decomposition
admits a decomposition 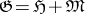 , where
, where 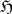 is the subalgebra corresponding to
is the subalgebra corresponding to 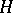 and
and 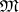 is a subspace that is invariant under
is a subspace that is invariant under 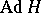 where
where 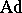 is the adjoint representation of
is the adjoint representation of  (cf. Adjoint representation of a Lie group). If
(cf. Adjoint representation of a Lie group). If 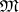 is identified with
is identified with 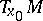 , then any
, then any 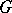 -invariant metric
-invariant metric 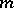 on
on  is obtained from some
is obtained from some 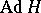 -invariant Euclidean metric
-invariant Euclidean metric 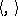 on
on 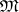 in the following way:
in the following way:
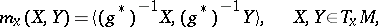 |
where 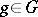 is such that
is such that  .
.
The tensor fields associated with a  -invariant metric (the curvature tensor, its covariant derivatives, etc.) are
-invariant metric (the curvature tensor, its covariant derivatives, etc.) are 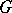 -invariant fields. In the case of a homogeneous space
-invariant fields. In the case of a homogeneous space 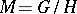 , their value at a point
, their value at a point 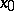 can be expressed in terms of the Nomizu operator
can be expressed in terms of the Nomizu operator  , which is defined by the formula
, which is defined by the formula
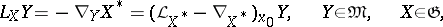 |
where 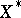 is the velocity field of the one-parameter group of transformations
is the velocity field of the one-parameter group of transformations 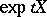 ,
,  is the covariant differentiation operator of the Riemannian connection and
is the covariant differentiation operator of the Riemannian connection and 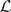 is the Lie derivative operator. In particular, the curvature operator
is the Lie derivative operator. In particular, the curvature operator 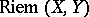 and the sectional curvature
and the sectional curvature 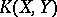 in the direction given by the orthonormal basis
in the direction given by the orthonormal basis 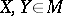 satisfy the following formulas:
satisfy the following formulas:
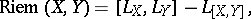 |
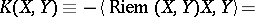 |
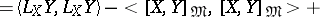 |
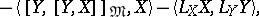 |
where 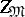 is the projection of
is the projection of 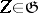 on
on 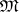 along
along 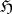 .
.
The Nomizu operators can be expressed in terms of the Lie algebra 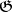 and the metric
and the metric 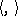 by the formula
by the formula
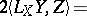 |
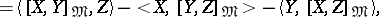 |
where 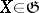 ,
, 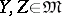 . It follows from the definition of the Nomizu operators that their action on
. It follows from the definition of the Nomizu operators that their action on  -invariant fields differs only in sign from that of the covariant derivative at the point
-invariant fields differs only in sign from that of the covariant derivative at the point 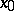 . If the Riemannian space
. If the Riemannian space 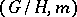 does not contain flat factors in the de Rham decomposition, then the linear Lie algebra generated by the Nomizu operators
does not contain flat factors in the de Rham decomposition, then the linear Lie algebra generated by the Nomizu operators 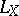 ,
, 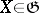 , is the same as the holonomy algebra (cf. Holonomy group) of the space
, is the same as the holonomy algebra (cf. Holonomy group) of the space 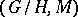 at
at 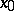 .
.
A description of the geodesics of an invariant metric on a homogeneous space can be given in the following way. Suppose, to begin with, that 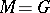 is a Lie group acting on itself by left translations. Let
is a Lie group acting on itself by left translations. Let 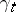 be a left-invariant geodesic of the metric
be a left-invariant geodesic of the metric 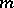 on the Lie group
on the Lie group  and let
and let 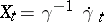 be the curve in the Lie algebra
be the curve in the Lie algebra 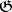 corresponding to it (the velocity hodograph). The curve
corresponding to it (the velocity hodograph). The curve 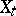 satisfies the hodograph equation
satisfies the hodograph equation
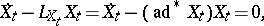 |
where 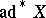 is the operator dual to the adjoint representation
is the operator dual to the adjoint representation 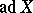 . The geodesic
. The geodesic 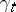 can be recovered in terms of its velocity hodograph
can be recovered in terms of its velocity hodograph 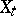 from the differential equation
from the differential equation 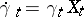 (which is linear if the group
(which is linear if the group 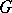 is linear) or from the functional relations
is linear) or from the functional relations
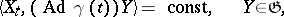 |
giving the first integrals of this equation. Thus, the description of the geodesics of the metric 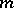 reduces to the integration of the hodograph equation, which sometimes can be completely integrated. For example, in the case when the metric
reduces to the integration of the hodograph equation, which sometimes can be completely integrated. For example, in the case when the metric 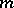 is also invariant with respect to right translations, the geodesics passing through the point
is also invariant with respect to right translations, the geodesics passing through the point  are the one-parameter subgroups of
are the one-parameter subgroups of 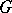 . Such a metric exists on any compact Lie group. In the case of an arbitrary homogeneous space
. Such a metric exists on any compact Lie group. In the case of an arbitrary homogeneous space 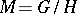 an invariant metric
an invariant metric 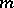 on
on 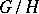 can be "lifted" to a left-invariant metric
can be "lifted" to a left-invariant metric 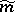 on
on 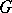 for which the natural bundle
for which the natural bundle 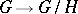 of the Riemannian space
of the Riemannian space 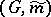 over the Riemannian space
over the Riemannian space 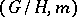 is a Riemannian bundle, that is, the length of tangent vectors orthogonal to the fibre remains unaltered under projection. For this it is sufficient to extend the metric
is a Riemannian bundle, that is, the length of tangent vectors orthogonal to the fibre remains unaltered under projection. For this it is sufficient to extend the metric 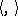 to the entire algebra
to the entire algebra 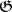 by setting
by setting
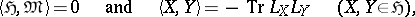 |
and carrying it over by left translations to a metric 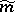 on
on  . The geodesics of
. The geodesics of  are projections of geodesics of
are projections of geodesics of 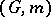 that are orthogonal to the fibres.
that are orthogonal to the fibres.
Since the function 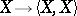 on
on 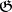 is always a first integral of the hodograph equation (the energy integral), the corresponding equation of the vector field on
is always a first integral of the hodograph equation (the energy integral), the corresponding equation of the vector field on 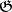 is tangent to the spheres
is tangent to the spheres 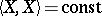 . This implies the completeness of the hodograph equation and therefore also the completeness of any invariant Riemannian metric on a homogeneous space. For a pseudo-Riemannian metric the completeness property does not hold, in general. On the other hand, any invariant pseudo-Riemannian metric on a compact homogeneous space is complete.
. This implies the completeness of the hodograph equation and therefore also the completeness of any invariant Riemannian metric on a homogeneous space. For a pseudo-Riemannian metric the completeness property does not hold, in general. On the other hand, any invariant pseudo-Riemannian metric on a compact homogeneous space is complete.
See also Symmetric space.
References
| [1] | S. Helgason, "Differential geometry, Lie groups, and symmetric spaces" , Acad. Press (1978) |
| [2] | A.Z. Petrov, "New methods in general relativity theory" , Moscow (1966) (In Russian) |
| [3] | S. Kobayashi, K. Nomizu, "Foundations of differential geometry" , 2 , Interscience (1969) |
| [4] | S. Kobayashi, "Transformation groups in differential geometry" , Springer (1972) |
| [5] | J.A. Wolf, "Spaces of constant curvature" , Publish or Perish (1984) |
| [6] | A. Lichnerowicz, "Geometry of groups of transformations" , Noordhoff (1977) (Translated from French) |
| [7] | A.L. Besse, "Einstein manifolds" , Springer (1987) |
Comments
A de Rham decomposition (of the tangent space 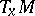 at a point
at a point  ) is defined as follows. Let
) is defined as follows. Let 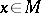 , let
, let 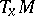 be the tangent space at
be the tangent space at  and let
and let 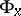 be the holonomy group of the Riemannian connection at
be the holonomy group of the Riemannian connection at  . The group
. The group 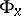 acts on
acts on 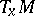 . Let
. Let 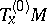 be the subspace of tangent vectors that are left invariant under
be the subspace of tangent vectors that are left invariant under  . Let
. Let 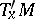 be the orthogonal complement of
be the orthogonal complement of 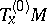 in
in 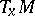 and let
and let 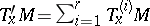 be a decomposition of
be a decomposition of  into mutually-orthogonal invariant irreducible subspaces. The decomposition
into mutually-orthogonal invariant irreducible subspaces. The decomposition
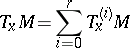 |
is called a de Rham decomposition or a canonical decomposition.
An irreducible Riemannian manifold is one for which the holonomy group 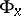 acts irreducibly on
acts irreducibly on 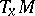 (so that there is only one factor in the Rham decomposition of
(so that there is only one factor in the Rham decomposition of 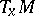 ).
).
The de Rham decomposition theorem says that a connected simply-connected complete Riemannian manifold  is isometric to a direct product
is isometric to a direct product 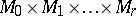 where
where 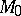 is a Euclidean space (possibly of dimension zero) and where the
is a Euclidean space (possibly of dimension zero) and where the 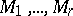 are all simply-connected complete irreducible Riemannian manifolds. Such a decomposition is unique up to the order of the factors, [a1], Sect. IV. 6.
are all simply-connected complete irreducible Riemannian manifolds. Such a decomposition is unique up to the order of the factors, [a1], Sect. IV. 6.
References
| [a1] | S. Kobayashi, K. Nomizu, "Foundations of differential geometry" , 1 , Interscience (1963) |
Invariant metric. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Invariant_metric&oldid=18868