Interpolation of operators
Obtaining from known properties of an operator in two or more spaces conclusions as to the properties of this operator in spaces that are in a certain sense intermediate. A Banach pair 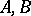 is a pair of Banach spaces (cf. Banach space) that are algebraically and continuously imbedded in a separable linear topological space
is a pair of Banach spaces (cf. Banach space) that are algebraically and continuously imbedded in a separable linear topological space  . One introduces the norm
. One introduces the norm
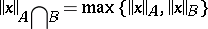 |
on the intersection 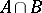 ; on the arithmetical sum
; on the arithmetical sum 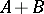 the norm
the norm
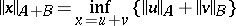 |
is introduced. The spaces 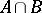 and
and 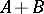 are Banach spaces. A Banach space
are Banach spaces. A Banach space 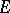 is said to be intermediate for the pair
is said to be intermediate for the pair 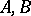 if
if 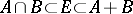 .
.
A linear mapping 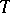 , acting from
, acting from 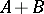 into
into 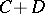 , is called a bounded operator from the pair
, is called a bounded operator from the pair  into the pair
into the pair  if its restriction to
if its restriction to 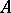 (respectively,
(respectively, 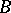 ) is a bounded operator from
) is a bounded operator from  into
into 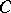 (respectively, from
(respectively, from 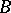 into
into 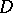 ). A triple of spaces
). A triple of spaces 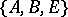 is called an interpolation triple relative to the triple
is called an interpolation triple relative to the triple 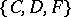 , where
, where 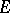 is intermediate for
is intermediate for 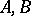 (respectively,
(respectively, 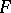 is intermediate for
is intermediate for 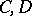 ), if every bounded operator from
), if every bounded operator from  into
into 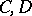 maps
maps 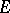 into
into 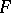 . If
. If 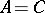 ,
, 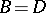 ,
, 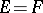 , then
, then 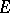 is called an interpolation space between
is called an interpolation space between  and
and 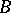 . For interpolation triples there exists a constant
. For interpolation triples there exists a constant  such that
such that
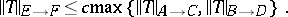 |
The first interpolation theorem was obtained by M. Riesz (1926): The triple 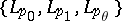 is an interpolation triple for
is an interpolation triple for 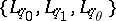 if
if 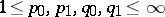 and if for a certain
and if for a certain 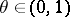 ,
,
 | (1) |
The measures in the listed spaces may be different for each triple. Analogues of these theorems for other classes of families of spaces need not hold; e.g., 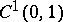 is not an interpolation space between
is not an interpolation space between 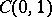 and
and 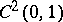 .
.
An interpolation functor 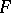 is a functor that assigns to each Banach pair
is a functor that assigns to each Banach pair 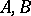 an intermediate space
an intermediate space  , where, moreover, for any two Banach pairs
, where, moreover, for any two Banach pairs 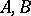 and
and 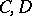 , the triples
, the triples 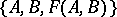 and
and  are interpolation for each other. There is a number of methods for constructing interpolation functors. Two of these gained the largest number of applications.
are interpolation for each other. There is a number of methods for constructing interpolation functors. Two of these gained the largest number of applications.
Peetre's 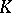 -method.
-method.
For a Banach pair 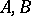 one constructs the functional
one constructs the functional
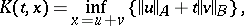 |
which is equivalent to the norm in 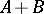 for each
for each  . A Banach space
. A Banach space 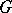 of measurable functions on the semi-axis is called an ideal space if
of measurable functions on the semi-axis is called an ideal space if 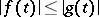 almost-everywhere on
almost-everywhere on 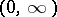 and
and  imply
imply 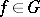 and
and 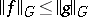 . One considers all elements
. One considers all elements  from
from 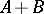 for which
for which 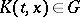 . They form the Banach space
. They form the Banach space 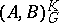 with the norm
with the norm 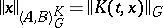 . The space
. The space 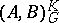 is non-empty and is intermediate for
is non-empty and is intermediate for 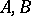 if and only if the function
if and only if the function 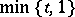 belongs to
belongs to 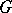 . In this case
. In this case 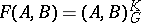 is an interpolation functor. For some Banach pairs the function
is an interpolation functor. For some Banach pairs the function 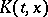 can be computed. This makes it possible to constructive effectively interpolation spaces. For
can be computed. This makes it possible to constructive effectively interpolation spaces. For  :
:
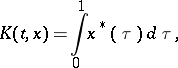 |
where 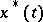 is a non-increasing right-continuous function on
is a non-increasing right-continuous function on 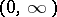 that is equi-measurable with the function
that is equi-measurable with the function  . For
. For 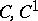 :
:
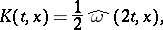 |
where 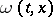 is the modulus of continuity (cf. Continuity, modulus of) of the function
is the modulus of continuity (cf. Continuity, modulus of) of the function  , and the sign
, and the sign  denotes transition to the least convex majorant on
denotes transition to the least convex majorant on 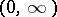 . For
. For 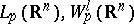 (a Sobolev space),
(a Sobolev space),
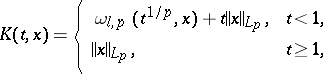 |
where
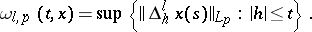 |
One often takes the space with norm
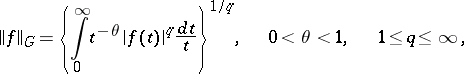 |
as 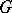 . The corresponding functor is denoted by
. The corresponding functor is denoted by 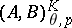 . The Besov spaces
. The Besov spaces
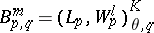 |
with 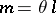 play an important role in the theory of partial differential equations. A number of classical inequalities in analysis can be made more precise in terms of the Lorentz spaces
play an important role in the theory of partial differential equations. A number of classical inequalities in analysis can be made more precise in terms of the Lorentz spaces
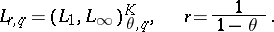 |
The complex method of Calderón–Lions.
Let 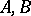 be a Banach pair. Denote by
be a Banach pair. Denote by 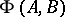 the space of all functions
the space of all functions 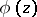 defined in the strip
defined in the strip 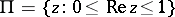 of the complex plane, with values in
of the complex plane, with values in 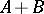 , and having the following properties: 1)
, and having the following properties: 1) 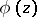 is continuous and bounded on
is continuous and bounded on 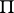 in the norm of
in the norm of 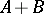 ; 2)
; 2) 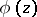 is analytic inside
is analytic inside 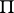 in the norm of
in the norm of  ; 3)
; 3) 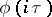 is continuous and bounded in the norm of
is continuous and bounded in the norm of 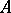 ; and 4)
; and 4) 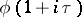 is continuous and bounded in the norm of
is continuous and bounded in the norm of 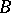 . The space
. The space 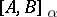 ,
, 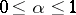 , is defined as the set of all elements
, is defined as the set of all elements 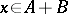 that can be represented as
that can be represented as 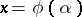 for
for 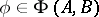 . In it one introduces the norm
. In it one introduces the norm
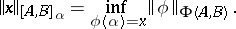 |
In this way the interpolation functor 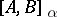 is defined. If
is defined. If 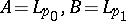 ,
, 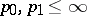 , then
, then  with
with  . If
. If 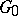 and
and  are two ideal spaces and if in at least one of them the norm is absolutely continuous, then
are two ideal spaces and if in at least one of them the norm is absolutely continuous, then 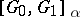 consists of all functions
consists of all functions 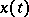 for which
for which 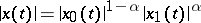 for some
for some 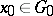 ,
, 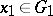 . If
. If 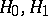 are two complex Hilbert spaces with
are two complex Hilbert spaces with 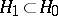 , then
, then 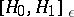 is a family of spaces that have very important applications. It is called a Hilbert scale. If
is a family of spaces that have very important applications. It is called a Hilbert scale. If  ,
, 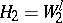 , then
, then 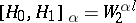 (a Sobolev space of fractional index). For other methods of constructing interpolation functors, as well as on their relation to the theory of scales of Banach spaces, see [1], [3], [5], [8], [9].
(a Sobolev space of fractional index). For other methods of constructing interpolation functors, as well as on their relation to the theory of scales of Banach spaces, see [1], [3], [5], [8], [9].
In the theory of interpolation of operators, Marcinkiewicz' interpolation theorem on interpolation operators of weak type plays an important role. An operator 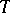 from a Banach space
from a Banach space 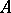 into a space of measurable functions, e.g. on the semi-axis, is called an operator of weak type
into a space of measurable functions, e.g. on the semi-axis, is called an operator of weak type 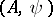 if
if 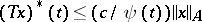 . It is assumed here that
. It is assumed here that 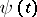 and
and 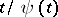 are non-decreasing functions (e.g.
are non-decreasing functions (e.g. 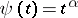 ,
, 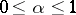 ). Theorems of Marcinkiewicz type enable one to describe for operators
). Theorems of Marcinkiewicz type enable one to describe for operators 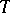 of weak types
of weak types 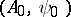 and
and 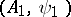 simultaneously (where
simultaneously (where 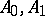 is a Banach pair) the pairs of spaces
is a Banach pair) the pairs of spaces 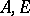 for which
for which 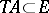 . In many cases it is sufficient to check that the operator
. In many cases it is sufficient to check that the operator
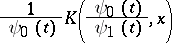 |
(where 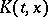 is the Peetre functional for
is the Peetre functional for  ) acts from
) acts from 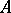 into
into 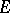 . If for all linear operators of weak types
. If for all linear operators of weak types 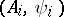 it has been shown that this functional acts from
it has been shown that this functional acts from 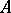 into
into 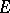 , then this also holds for quasi-additive operators (i.e. with the property
, then this also holds for quasi-additive operators (i.e. with the property 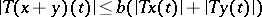 ) of weak types
) of weak types  ,
, 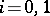 . Many important operators in analysis (e.g. Hilbert's singular operator) are of weak types in natural spaces; hence the corresponding interpolation theorems have found numerous applications.
. Many important operators in analysis (e.g. Hilbert's singular operator) are of weak types in natural spaces; hence the corresponding interpolation theorems have found numerous applications.
References
| [1] | P. Butzer, H. Berens, "Semi-groups of operators and approximation" , Springer (1967) |
| [2] | A. Zygmund, "Trigonometric series" , 2 , Cambridge Univ. Press (1988) |
| [3] | S.G. Krein, Yu.I. Petunin, E.M. Semenov, "Interpolation of linear operators" , Amer. Math. Soc. (1982) (Translated from Russian) |
| [4] | J.L. Lions, E. Magenes, "Non-homogenous boundary value problems and applications" , 1–2 , Springer (1972) (Translated from French) |
| [5] | E. Magenes, "Spazi di interpolazione ed equazioni a derivate parziali" , Conf. VII Congr. Union Mat. Italy, 1963 , Cremonese (1965) pp. 134–197 |
| [6] | E.M. Stein, G. Weiss, "Introduction to Fourier analysis on Euclidean spaces" , Princeton Univ. Press (1971) |
| [7] | N.Ya. Vilenkin (ed.) et al. (ed.) , Functional analysis , Wolters-Noordhoff (1972) (Translated from Russian) |
| [8] | J. Bergh, B.I. Löfström, "Interpolation spaces" , Springer (1976) |
| [9] | H. Triebel, "Interpolation theory, function spaces, differential operators" , North-Holland (1978) |
Comments
The theorem of M. Riesz mentioned in the main article is often called the M. Riesz convexity theorem. It has a somewhat more precise statement as follows (involving a bound on a certain norm for the bounded operator in question). Let 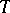 be a linear operator mapping a linear space
be a linear operator mapping a linear space  of complex-valued measurable functions on a measure space
of complex-valued measurable functions on a measure space 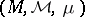 into measurable functions on another measure space
into measurable functions on another measure space 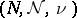 . Assume
. Assume  contains all indicator functions of measurable sets and is such that whenever
contains all indicator functions of measurable sets and is such that whenever 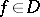 , then also all truncations (i.e. functions which coincide with
, then also all truncations (i.e. functions which coincide with 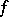 in
in 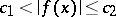 for certain
for certain 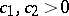 and vanish elsewhere) belong to
and vanish elsewhere) belong to 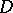 . The operator
. The operator 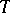 is said to be of type (
is said to be of type (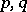 ) if there is a constant
) if there is a constant 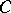 such that
such that
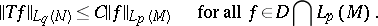 | (a1) |
The least  for which (a1) holds is called the
for which (a1) holds is called the 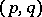 -norm of
-norm of 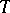 . The M. Riesz convexity theorem now states: If a linear operator
. The M. Riesz convexity theorem now states: If a linear operator 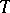 is of types
is of types 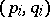 with
with 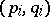 -norms
-norms 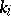 ,
, 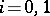 , then
, then 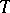 is of type
is of type 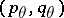 with
with 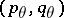 -norm
-norm 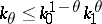 , provided
, provided 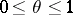 and
and 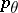 ,
, 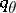 satisfy (1). (The name "convexity theorem" derives from the fact that the
satisfy (1). (The name "convexity theorem" derives from the fact that the 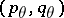 -norm of
-norm of 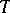 , as a function of
, as a function of 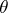 , is logarithmically convex.)
, is logarithmically convex.)
In the same setting, 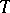 is called subadditive if
is called subadditive if
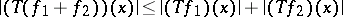 |
for almost-all 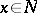 and for
and for 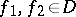 . A subadditive operator
. A subadditive operator  is said to be of weak type (
is said to be of weak type (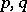 ) (where
) (where 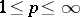 ,
, 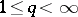 ) if there is a constant
) if there is a constant 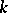 such that
such that
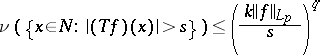 | (a2) |
for all 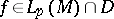 . The least
. The least 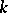 for which (a2) holds is called the weak (
for which (a2) holds is called the weak ( )-norm of
)-norm of 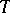 . (Note that the left-hand side of (a2) is the so-called distribution function of
. (Note that the left-hand side of (a2) is the so-called distribution function of 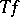 .) For
.) For 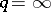 , (a2) must be replaced by
, (a2) must be replaced by 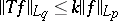 .
.
A still further generalization is that of an operator of restricted weak type  , cf. [6].
, cf. [6].
Singular integral operators (cf. Singular integral) often prove to be of some (weak) type (e.g. the Hilbert transform is of weak type 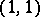 ).
).
References
| [a1] | C. Bennett, R.C. Sharpley, "Interpolation of operators" , Acad. Press (1988) |
Interpolation of operators. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Interpolation_of_operators&oldid=47394