Integral exponential function
The special function defined for real 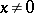 by the equation
by the equation
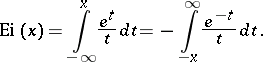 |
The graph of the integral exponential function is illustrated in Fig..
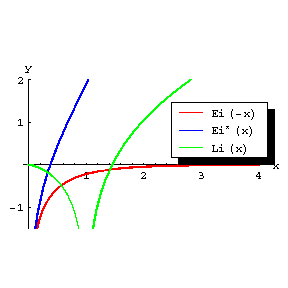
Figure: i051440a
Graphs of the functions 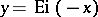 ,
, 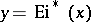 and
and 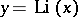 .
.
For 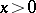 , the function
, the function 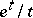 has an infinite discontinuity at
has an infinite discontinuity at 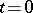 , and the integral exponential function is understood in the sense of the principal value of this integral:
, and the integral exponential function is understood in the sense of the principal value of this integral:
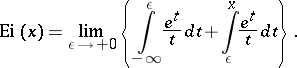 |
The integral exponential function can be represented by the series
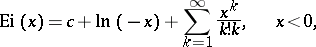 | (1) |
and
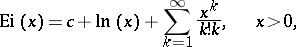 | (2) |
where 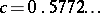 is the Euler constant.
is the Euler constant.
There is an asymptotic representation:
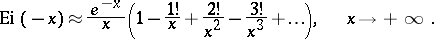 |
As a function of the complex variable  , the integral exponential function
, the integral exponential function
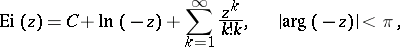 |
is a single-valued analytic function in the  -plane slit along the positive real semi-axis
-plane slit along the positive real semi-axis 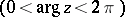 ; here the value of
; here the value of 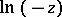 is chosen such that
is chosen such that 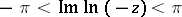 . The behaviour of
. The behaviour of 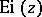 close to the slit is described by the limiting relations:
close to the slit is described by the limiting relations:
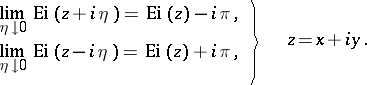 |
The asymptotic representation in the region 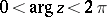 is:
is:
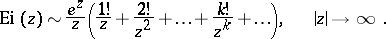 |
The integral exponential function is related to the integral logarithm 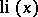 by the formulas
by the formulas
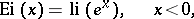 |
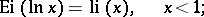 |
and to the integral sine 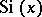 and the integral cosine
and the integral cosine 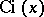 by the formulas:
by the formulas:
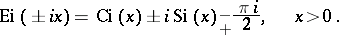 |
The differentiation formula is:
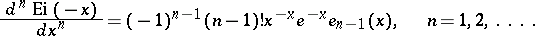 |
The following notations are sometimes used:
 |
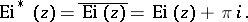 |
References
| [1] | H. Bateman (ed.) A. Erdélyi (ed.) et al. (ed.) , Higher transcendental functions , 2. Bessel functions, parabolic cylinder functions, orthogonal polynomials , McGraw-Hill (1953) |
| [2] | E. Jahnke, F. Emde, "Tables of functions with formulae and curves" , Dover, reprint (1945) (Translated from German) |
| [3] | A. Krazer, W. Franz, "Transzendente Funktionen" , Akademie Verlag (1960) |
| [4] | N.N. Lebedev, "Special functions and their applications" , Prentice-Hall (1965) (Translated from Russian) |
Comments
The function 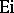 is usually called the exponential integral.
is usually called the exponential integral.
Instead of by the series representation, for complex values of  (
( not positive real) the function
not positive real) the function 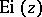 can be defined by the integal (as for real
can be defined by the integal (as for real 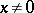 ); since the integrand is analytic, the integral is path-independent in
); since the integrand is analytic, the integral is path-independent in 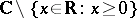 .
.
Formula (1) with  replaced by
replaced by  then holds for
then holds for 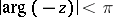 , and the function defined by (2) (for
, and the function defined by (2) (for 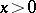 ) is also known as the modified exponential integral.
) is also known as the modified exponential integral.
Integral exponential function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Integral_exponential_function&oldid=47371