Incidence coefficient

A number characterizing the coherence of the orientations of incident elements of simplicial, polyhedral (CW-) and other complexes. The concept of the incidence coefficient and its properties necessarily enter into the definition of an arbitrary abstract complex (cf. Complex (in homological algebra)).

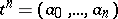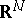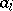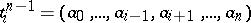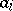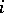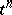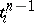Let be an oriented simplex in , i.e. a simplex in which a definite order of its vertices has been chosen, and let be its oriented face opposite to . If is even, then and are coherently oriented, and the orientation of 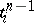is induced by the orientation of 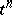; in this case they are assigned the incidence coefficient 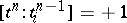. If 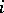is odd, then 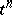and 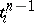are non-coherently oriented, and they are assigned the incidence coefficient .

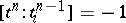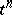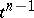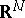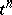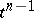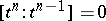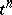Suppose now that and are elements (simplices) of a simplicial complex in . Then their incidence coefficient is defined as follows. If and are not incident, then ; if and 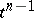are incident, then 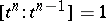or 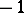, depending on whether they are coherently oriented or not.

Properties of incidence coefficients.

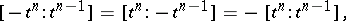(1)

where 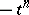is the oppositely-oriented simplex, i.e. the simplex oriented by an odd permutation of the vertices of ;

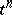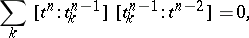(2)

where the summation extends over all oriented simplices 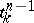(for some definitions of a simplicial complex (2) holds only if completeness is required).

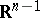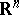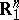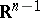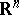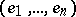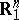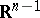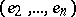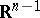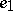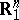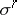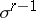Analogously, for a suitable definition of coherence of orientation the incidence coefficient of two elements of a polyhedral complex can be defined. Let be a subspace in , let be one of the half-spaces bounded by , and let in be chosen an oriented vector basis . Then and are called coherently oriented if is a basis in and is directed into . Two cells and are coherently oriented if they are contained in a certain coherently-oriented half-space and subspace, respectively.

References

[1]	P.S. Aleksandrov, "An introduction to homological dimension theory and general combinatorial topology" , Moscow (1975) (In Russian)
[2]	P.J. Hilton, S. Wylie, "Homology theory. An introduction to algebraic topology" , Cambridge Univ. Press (1960)
[3]	A. Dold, "Lectures on algebraic topology" , Springer (1980)