Hotelling test
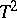 -test
-test
A test intended for testing a hypothesis 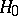 according to which the true value of the unknown vector
according to which the true value of the unknown vector 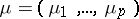 of mathematical expectation of a non-degenerate
of mathematical expectation of a non-degenerate 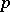 -dimensional normal law
-dimensional normal law 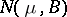 whose covariance matrix
whose covariance matrix  is also unknown, is the vector
is also unknown, is the vector 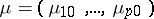 . Hotelling's test is based on the following result. Let
. Hotelling's test is based on the following result. Let 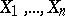 be independent
be independent 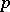 -dimensional random vectors,
-dimensional random vectors, 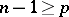 , subject to the non-degenerate normal law
, subject to the non-degenerate normal law 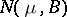 , and let
, and let
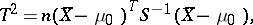 |
where
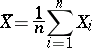 |
and
 |
are maximum-likelihood estimators for the unknown parameters 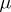 and
and 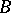 . Then the statistic
. Then the statistic
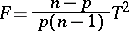 |
has the non-central Fisher 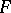 -distribution with
-distribution with 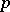 and
and  degrees of freedom and non-centrality parameter
degrees of freedom and non-centrality parameter
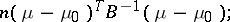 |
the statistic 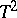 has the Hotelling
has the Hotelling 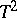 -distribution. Consequently, to test the hypothesis
-distribution. Consequently, to test the hypothesis 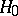 :
: 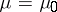 against the alternative
against the alternative 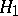 :
: 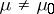 one can compute the values of the statistic
one can compute the values of the statistic 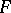 based on realizations of the independent random vectors
based on realizations of the independent random vectors 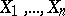 from the non-degenerate
from the non-degenerate 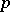 -dimensional normal law
-dimensional normal law 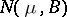 , which under the hypothesis
, which under the hypothesis 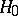 has the central
has the central 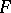 -distribution with
-distribution with 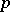 and
and 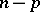 degrees of freedom. Using Hotelling's test with significance level
degrees of freedom. Using Hotelling's test with significance level 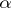 ,
, 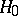 must be rejected if
must be rejected if 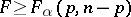 , where
, where 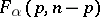 is the
is the 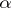 -quantile of the
-quantile of the 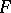 -distribution. The connection between Hotelling's test and the generalized likelihood-ratio test should be mentioned. Let
-distribution. The connection between Hotelling's test and the generalized likelihood-ratio test should be mentioned. Let
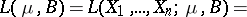 |
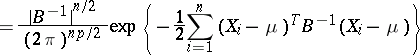 |
be the likelihood function computed from the sample 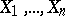 . The generalized likelihood-ratio test for testing the simple hypothesis
. The generalized likelihood-ratio test for testing the simple hypothesis 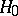 :
: 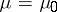 against the compound alternative
against the compound alternative 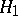 :
: 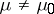 is constructed from the statistic
is constructed from the statistic
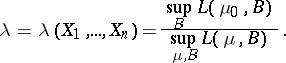 |
The statistic 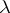 and the statistics
and the statistics 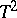 and
and 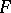 are related by:
are related by:
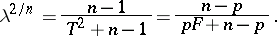 |
For testing the hypothesis 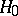 :
: 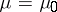 , Hotelling's test is uniformly most powerful among all tests that are invariant under similarity transformations (see Most-powerful test; Invariant test).
, Hotelling's test is uniformly most powerful among all tests that are invariant under similarity transformations (see Most-powerful test; Invariant test).
References
| [1] | T.W. Anderson, "An introduction to multivariate statistical analysis" , Wiley (1984) |
| [2] | C.R. Rao, "Linear statistical inference and its applications" , Wiley (1973) |
Hotelling test. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hotelling_test&oldid=47275