Homogeneous operator
From Encyclopedia of Mathematics
A mapping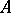 
of a vector space 
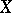into a vector space 
such that there exists a symmetric multilinear mapping
 |
with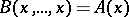 
. The number 
of variables 
is called the degree of the homogeneous operator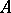 
. A linear operator 
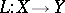is a homogeneous operator of degree 1 (usually just called homogeneous). One writes 
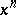instead of 
for short, meaning by this the element of 
with all coordinates equal, but not a power of an element — a concept that is not defined in an arbitrary vector space. If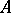 
is a homogeneous operator of degree 
, then
 |
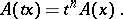More generally:
 |
 |
If 
and 
are normed vector spaces, then 
is continuous if and only if it is bounded, and if 
is continuous at zero it is continuous on the whole of 
.
References
| [1] | L.A. Lyusternik, V.I. Sobolev, "Elements of functional analysis" , Hindushtan Publ. Comp. (1974) (Translated from Russian) |
| [2a] | H. Cartan, "Calcul différentiel" , Hermann (1967) |
| [2b] | H. Cartan, "Differential forms" , Kershaw (1983) (Translated from French) |
How to Cite This Entry:
Homogeneous operator. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Homogeneous_operator&oldid=47254
Homogeneous operator. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Homogeneous_operator&oldid=47254
This article was adapted from an original article by V.I. Sobolev (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article