Grammar form

A (phrase-structure) grammar (cf. also Grammar system) 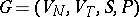, viewed as a source of structurally similar grammars. (See Formal languages and automata.) The languages generated by the latter grammars give rise to a family 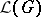of languages. (See also Abstract family of languages.) Grammars viewed in this fashion, as generators of structurally similar grammars and their languages, are referred to as grammar forms.

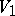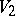Let and be alphabets. A disjoint-finite-letter substitution (dfl-substitution) is a mapping 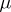of 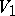into the set of non-empty subsets of 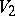such that 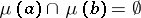for all distinct . Thus, a dfl-substitution associates one or more letters of 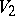to each letter of , and no letter of 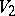is associated to two letters of 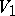. Because 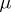is a substitution, its domain is immediately extended to concern words and languages over 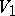. For a production 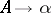, one defines

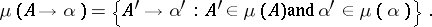A grammar 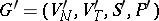is an interpretation of a grammar 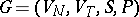modulo 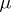, denoted by 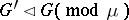, where 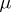is a dfl-substitution on 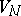, if the following conditions are satisfied:

i) 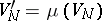, 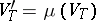and ;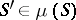

ii) 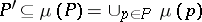. The grammar 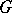is referred to as the master or form grammar, while 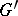is the image or interpretation grammar. The grammar family and the grammatical (language) family of 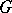are defined by

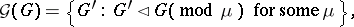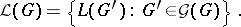A language family 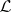is termed grammatical if 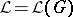, for some 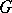. Two grammars are form equivalent if their language families coincide. They are strongly form-equivalent if their grammar families coincide.

Operationally one obtains an interpretation grammar by mapping terminals and non-terminals of the form grammar into disjoint sets of terminals and non-terminals, respectively, then extending the mapping to concern productions and, finally, taking a subset of the resulting production set. The last-mentioned point is especially important: great flexibility results because it is possible to omit productions.

A grammar is said to be a grammar form if it is used within the framework of interpretations. There is no difference between a grammar and a grammar form as constructs.

Strong form equivalence is decidable, whereas form equivalence is undecidable even for context-free grammar forms. To characterize the grammar forms giving rise to a specific language family, e.g., the family of context-free languages, is equivalent to characterizing all possible normal forms for the corresponding grammars, e.g., all possible normal forms for context-free grammars. (For further details, see [a5]. [a1] and [a2] represent early developments.)

In spite of the discrete framework of formal languages, grammatical families possess remarkable density properties. For instance, if 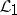is a grammatical family containing all regular languages and 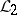is a grammatical family such that 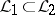, then there is a grammatical family 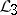with the property 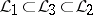. (See [a3], [a4], [a5], and [a6] for a connection with graph colouring.) A theory analogous to grammar forms has been developed also for parallel rewriting. (See 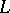-systems, [a5].)

References

[a1]	A.B. Cremers, S. Ginsburg, "Context-free grammar forms" J. Comput. System Sci. , 11 (1975) pp. 86–116 MR0375848 Zbl 0328.68071
[a2]	H.A. Maurer, M. Penttonen, A. Salomaa, D. Wood, "On non context-free grammar forms" Math. Systems Th. , 12 (1979) pp. 297–324 MR0541861 Zbl 0415.68036
[a3]	A. Salomaa, H.A. Maurer, D. Wood, "Dense hierarchies of grammatical families" J. Assoc. Comput. Mach. , 29 (1982) pp. 118–126 MR0662614 Zbl 0491.68077
[a4]	V. Niemi, "Density of grammar forms, I; II" Internat. J. Comput. Math. , 20 (1986) pp. 3–21; 91–114 Zbl 0655.68098
[a5]	Gh. Păun, A. Salomaa, "Families generated by grammars and L systems" G. Rozenberg (ed.) A. Salomaa (ed.) , Handbook of Formal Languages , 1 , Springer (1997) pp. 811–861 MR1470004
[a6]	A. Salomaa, "On color-families of graphs" Ann. Acad. Sci. Fennicae , AI6 (1981) pp. 135–148 MR0639971 Zbl 0497.05027