Genus of an entire function
From Encyclopedia of Mathematics
The integer equal to the larger of the two numbers 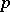 and
and 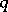 in the representation of the entire function
in the representation of the entire function 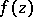 in the form
in the form
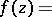 | (*) |
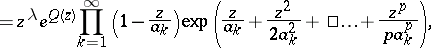 |
where 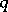 is the degree of the polynomial
is the degree of the polynomial 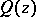 and
and 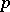 is the least integer satisfying the condition
is the least integer satisfying the condition
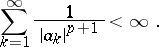 |
The number 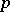 is called the genus of the product appearing in formula (*).
is called the genus of the product appearing in formula (*).
References
| [1] | B.Ya. Levin, "Distribution of zeros of entire functions" , Amer. Math. Soc. (1964) (Translated from Russian) |
Comments
The genus plays a role in factorization theorems for entire functions, cf. e.g. Hadamard theorem; Weierstrass theorem.
References
| [a1] | R.P. Boas, "Entire functions" , Acad. Press (1954) |
How to Cite This Entry:
Genus of an entire function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Genus_of_an_entire_function&oldid=47082
Genus of an entire function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Genus_of_an_entire_function&oldid=47082
This article was adapted from an original article by A.F. Leont'ev (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article