Gell-Mann-Dashen algebra

An infinite-dimensional Lie algebra occurring in quantum field theory. Let 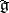be a finite-dimensional Lie algebra and 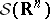the space of Schwartz test functions (cf. Generalized functions, space of). The Lie algebra 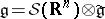is defined by

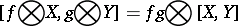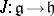and can be interpreted as the Lie algebra of the group of gauge transformations (cf. Gauge transformation) [a1]. Representations of are called current algebras in quantum field theory. Let be a homomorphism of Lie algebras and let 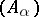be a basis of 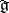with structure constants . The mapping 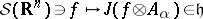defines an 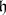-valued distribution 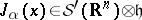and it is true that

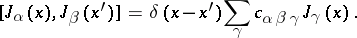Passing to the Fourier image one sets 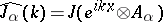for ; then

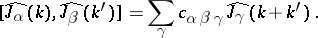R. Dashen and M. Gell-Mann (1966) studied and applied the latter commutation relations in the particular case when 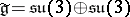, [a2].

General references for current algebras are [a3], [a4].

References

[a1]	R. Hermann, "Lie algebras and quantum mechanics" , Benjamin (1970)
[a2]	R. Dashen, M. Gell-Mann, "Representation of local current algebra at infinite momentum" Phys. Rev. Lett. , 17 (1966) pp. 340–343
[a3]	S.L. Adler, R. Dashen, "Current algebras" , Benjamin (1968)
[a4]	B. Renner, "Current algebras and their applications" , Pergamon (1968)