Fundamental matrix
matrizant
The transition matrix 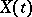 of solutions of a system of linear ordinary differential equations
of solutions of a system of linear ordinary differential equations
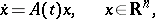 | (*) |
normalized at the point 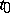 . The fundamental matrix is the unique continuous solution of the matrix initial value problem
. The fundamental matrix is the unique continuous solution of the matrix initial value problem
 |
(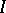 denotes the identity matrix) if the matrix-valued function
denotes the identity matrix) if the matrix-valued function 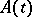 is locally summable over some interval
is locally summable over some interval 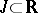 ,
, 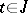 .
.
Every matrix 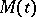 built of column-solutions
built of column-solutions 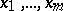 of the system (*), where
of the system (*), where 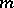 is a natural number, is expressible as
is a natural number, is expressible as 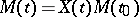 . In particular, every solution
. In particular, every solution 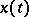 of (*) can be written in the form
of (*) can be written in the form 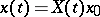 .
.
The expansion
 |
which converges absolutely for every 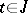 and uniformly on every compact interval in
and uniformly on every compact interval in 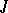 , and the Liouville–Ostrogradski formula
, and the Liouville–Ostrogradski formula
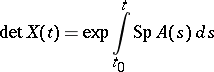 |
are valid. If the matrix 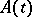 satisfies the Lappo-Danilevskii condition
satisfies the Lappo-Danilevskii condition
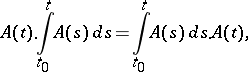 |
then
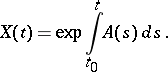 |
In particular, if 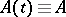 is a constant matrix, then
is a constant matrix, then
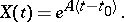 |
If 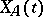 is the fundamental matrix of the system (*) with matrix
is the fundamental matrix of the system (*) with matrix 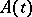 , then
, then
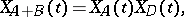 |
where
 |
The fundamental matrix makes it possible to write every solution of the inhomogeneous system
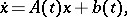 |
in which the function 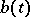 is locally summable on
is locally summable on 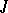 , in the form of Cauchy's formula
, in the form of Cauchy's formula
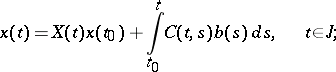 |
here
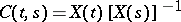 |
is called the Cauchy matrix of (*). The Cauchy matrix  is jointly continuous in its arguments on
is jointly continuous in its arguments on 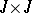 and for arbitrary
and for arbitrary 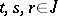 it has the properties
it has the properties
1) 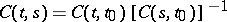 ;
;
2)  ;
;
3) 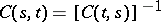 ;
;
4) 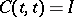 ;
;
5) 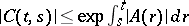 ,
, 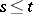 , where
, where  is the norm in
is the norm in 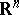 ;
;
6) if 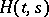 is the Cauchy matrix of the adjoint system
is the Cauchy matrix of the adjoint system
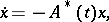 |
then
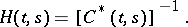 |
References
| [1] | N. Bourbaki, "Elements of mathematics. Functions of a real variable" , Addison-Wesley (1976) (Translated from French) |
| [2] | F.R. [F.R. Gantmakher] Gantmacher, "The theory of matrices" , 1 , Chelsea, reprint (1977) (Translated from Russian) |
| [3] | B.P. Demidovich, "Lectures on the mathematical theory of stability" , Moscow (1967) (In Russian) |
| [4] | V.A. Yakubovich, V.M. Starzhinskii, "Linear differential equations with periodic coefficients" , Wiley (1975) (Translated from Russian) |
Comments
The term "matrizant" is no longer in common use; instead the term "transition matrixtransition matrix" has become popular for what is called above "fundamental matrix" . See also Fundamental system of solutions.
Cauchy's formula is often called the variation of constants formula, and the Cauchy matrix is also called the transition matrix (cf. also Cauchy matrix).
References
| [a1] | R.W. Brockett, "Finite dimensional linear systems" , Wiley (1970) |
| [a2] | J.K. Hale, "Ordinary differential equations" , Wiley (1980) |
Fundamental matrix. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fundamental_matrix&oldid=47026