Fourier transform of a generalized function
An extension of the Fourier transform from test functions to generalized functions (cf. Generalized function). Let 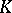 be a space of test functions on which the Fourier transformation
be a space of test functions on which the Fourier transformation 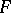 ,
,
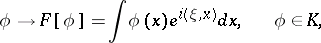 |
is defined and on which 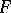 is an isomorphism of
is an isomorphism of 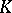 onto a space of test functions
onto a space of test functions 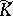 . Then the Fourier transformation
. Then the Fourier transformation 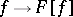 is defined on the space of generalized functions
is defined on the space of generalized functions 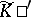 by
by
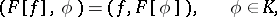 |
and this is an isomorphism of 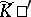 onto the space of generalized functions
onto the space of generalized functions 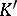 .
.
Examples.
1) 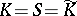 ,
, 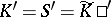 . Here the inverse of
. Here the inverse of 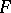 is the operation
is the operation
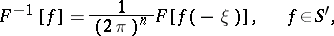 |
and the basic formulas for 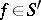 are
are
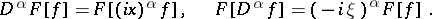 |
2) Let 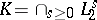 ,
, 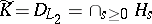 ,
, 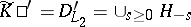 , where
, where 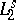 is the set of all functions
is the set of all functions 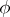 for which
for which  , and where
, and where 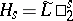 ,
, 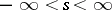 .
.
3)  ,
, 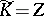 , where
, where 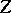 is the set of all entire functions
is the set of all entire functions 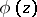 satisfying the growth condition: There is a number
satisfying the growth condition: There is a number 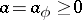 such that for any
such that for any 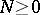 one can find a
one can find a 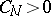 such that
such that
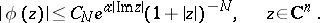 |
Fourier series of generalized functions.
If a generalized function 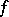 is periodic with
is periodic with  -period
-period 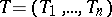 ,
, 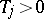 , then
, then 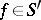 and it can be expanded in a trigonometric series,
and it can be expanded in a trigonometric series,
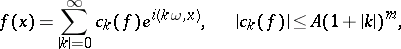 |
converging to 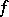 in
in 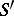 ; here
; here
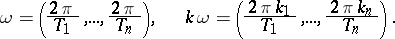 |
Examples.
4) 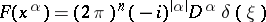 , in particular
, in particular 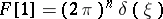 .
.
5) 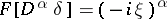 , in particular
, in particular 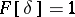 .
.
6) 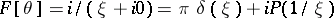 , where
, where 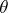 is the Heaviside function.
is the Heaviside function.
The Fourier transform of the convolution of generalized functions.
Let the direct product 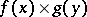 of two generalized functions
of two generalized functions 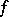 and
and 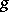 in
in 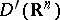 admit an extension to functions of the form
admit an extension to functions of the form 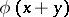 , for all
, for all 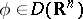 . Namely, suppose that for any sequence
. Namely, suppose that for any sequence  ,
, 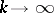 , in
, in 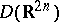 with the properties:
with the properties:  ,
, 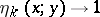 ,
, 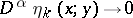 ,
,  ,
, 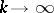 (uniformly on any compact set), the sequence
(uniformly on any compact set), the sequence
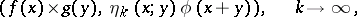 |
has a limit, denoted by 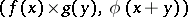 , which does not depend on the sequence
, which does not depend on the sequence 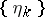 from the class indicated. In this case the functional
from the class indicated. In this case the functional  that acts according to the formula
that acts according to the formula 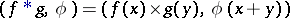 ,
,  , is called the convolution of the generalized functions
, is called the convolution of the generalized functions 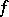 and
and  ,
, 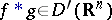 . The convolution does not exist for all pairs of generalized functions
. The convolution does not exist for all pairs of generalized functions 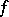 and
and 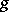 . It automatically exists if for any
. It automatically exists if for any 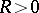 the set
the set
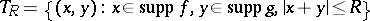 |
is bounded in 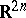 (in particular if
(in particular if 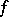 or
or 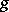 has compact support). If the convolution
has compact support). If the convolution  exists, then it is commutative:
exists, then it is commutative: 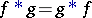 ; and it commutes with shifts and with derivatives:
; and it commutes with shifts and with derivatives: 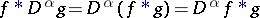 ; the Dirac
; the Dirac 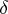 -function plays the role of "identity" :
-function plays the role of "identity" :  . Convolution is a non-associative operation. However, there are associative (and commutative) convolution algebras. The Dirac delta-function
. Convolution is a non-associative operation. However, there are associative (and commutative) convolution algebras. The Dirac delta-function 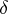 serves as the identity in them. For example, the set
serves as the identity in them. For example, the set 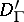 consisting of generalized functions from
consisting of generalized functions from 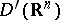 with support in a convex, acute, closed cone
with support in a convex, acute, closed cone 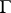 with vertex at
with vertex at  is a convolution algebra. The set
is a convolution algebra. The set 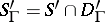 forms a convolution subalgebra of
forms a convolution subalgebra of 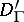 . Notation:
. Notation: 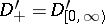 ,
, 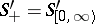 (when
(when 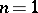 ). The formula for the Fourier transform of the convolution
). The formula for the Fourier transform of the convolution
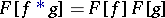 |
is valid in the following cases:
a) 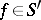 ,
, 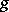 has compact support;
has compact support;
b) 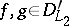 ;
;
c) 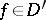 ,
, 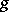 has compact support;
has compact support;
d) 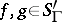 . In this case the product
. In this case the product 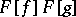 of the generalized functions
of the generalized functions 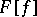 and
and 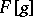 is understood to be the limit in
is understood to be the limit in 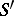 of the product
of the product 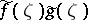 ,
, 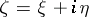 , as
, as 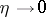 ,
,  , where
, where 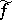 and
and 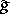 denote the Laplace transforms of
denote the Laplace transforms of 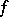 and
and 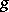 (see Generalized functions, product of).
(see Generalized functions, product of).
References
| [1] | V.S. Vladimirov, "Generalized functions in mathematical physics" , MIR (1979) (Translated from Russian) |
| [2] | I.M. Gel'fand, G.E. Shilov, "Generalized functions" , 1 , Acad. Press (1964) (Translated from Russian) |
| [3] | L. Schwartz, "Théorie des distributions" , 2 , Hermann (1951) |
| [4] | P. Antosik, J. Mikusiński, R. Sikorski, "Theory of distributions. The sequential approach" , Elsevier (1973) |
| [5] | L.V. Hörmander, "The analysis of linear partial differential operators" , 1 , Springer (1983) |
Comments
For other normalizations used in defining Fourier transforms, cf. Fourier transform.
The Heaviside function 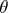 on
on 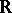 is defined by
is defined by 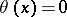 if
if 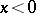 and
and 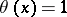 if
if 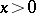 .
.
References
| [a1] | K. Yosida, "Functional analysis" , Springer (1980) pp. Chapt. 8, Sect. 4; 5 |
| [a2] | D.S. Jones, "The theory of generalized functions" , Cambridge Univ. Press (1982) |
Fourier transform of a generalized function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fourier_transform_of_a_generalized_function&oldid=46966