Federer spectral sequence
The Federer spectral sequence is a means to compute homotopy groups of function spaces (track groups; cf. Homotopy group). Its 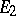 -stage consists of the singular cohomology (cf. Singular homology) of the source with coefficients in the homotopy groups of the target.
-stage consists of the singular cohomology (cf. Singular homology) of the source with coefficients in the homotopy groups of the target.
More specifically, let 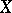 and
and 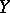 be connected topological spaces (cf. Connected space) and
be connected topological spaces (cf. Connected space) and 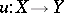 a continuous mapping. The Federer spectral sequence for this situation is a second quadrant homology spectral sequence
a continuous mapping. The Federer spectral sequence for this situation is a second quadrant homology spectral sequence 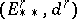 , with
, with
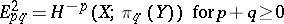 |
and 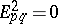 otherwise. Under appropriate finiteness conditions it converges to the homotopy group
otherwise. Under appropriate finiteness conditions it converges to the homotopy group 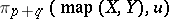 of the space of continuous mappings from
of the space of continuous mappings from 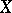 to
to 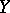 .
.
In the literature, this spectral sequence occurs explicitly in [a1] and implicitly in [a2] (and is for this reason sometimes referred to as the Barratt–Federer spectral sequence). See [a3] or [a4] for later generalizations and modifications.
References
| [a1] | H. Federer, "A study of function spaces by spectral sequences" Trans. Amer. Math. Soc. , 82 (1956) pp. 340–361 |
| [a2] | M.G. Barratt, "Track groups I, II" Proc. London Math. Soc. , 5 (1955) pp. 71–106; 285–329 |
| [a3] | R. Brown, "On Künneth suspensions" Proc. Cambridge. Philos. Soc. , 60 (1964) pp. 713–720 |
| [a4] | J.M. Møller, "On equivariant function spaces" Pacific J. Math. , 142 (1990) pp. 103–119 |
Federer spectral sequence. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Federer_spectral_sequence&oldid=46909