Extended complex plane

The complex -plane 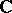compactified by adding the point 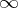at infinity and written as 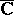. The exterior of any circle in 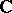, that, is, any set of the form , , 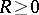becomes a neighbourhood of 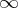. The extended complex plane is the Aleksandrov compactification of the plane 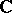, and is both homeomorphic and conformally equivalent to the Riemann sphere. The spherical, or chordal, metric on 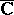is given by

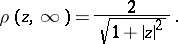References

[1]	A.I. Markushevich, "Theory of functions of a complex variable" , 1–2 , Chelsea (1977) (Translated from Russian)
[2]	B.V. Shabat, "Introduction of complex analysis" , 1–2 , Moscow (1976) (In Russian)

References

[a1]	J.B. Conway, "Functions of one complex variable" , Springer (1978)