Engel theorem

Suppose that for a finite-dimensional Lie algebra 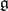over a field 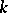the linear operators

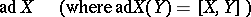are nilpotent for all 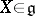. Then there is a basis of 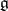in which the matrices of all operators 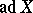are triangular with zeros on the main diagonal.

F. Engel proved (around 1887, published in [1]) that a Lie algebra 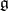with this property is solvable, from which, by a theorem of S. Lie (cf. Lie theorem), the assertion stated above follows immediately. The first published proof of Engel's theorem is due to W. Killing [2], who acknowledges Engel's priority. 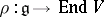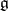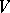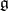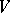Engel's theorem is often stated in the following more general form: If is a linear representation of a finite-dimensional Lie algebra in a vector space (where and are regarded over an arbitrary field) and if 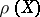is a nilpotent endomorphism for any 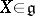, then there is a non-zero vector 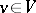such that 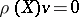for any 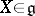. If is finite-dimensional, this implies the existence of a basis in 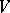in which all the 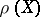have triangular matrices with zeros on the main diagonal (or, what is the same, there is a complete flag 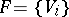in 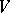for which 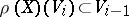for all 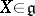and 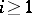). The conclusion of Engel's theorem is also true for any representation 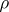for which the Lie algebra 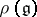is the linear hull of a subset consisting of nilpotent endomorphisms and that is closed under the operation of commutation. A Lie algebra 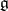is called an Engel algebra if any 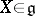is an Engel element, that is, if all the operators 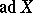, , 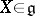are nilpotent or, what is the same, if for any there is an such that

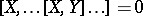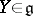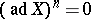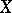( brackets) for any . A finite-dimensional Lie algebra is an Engel algebra if and only if it is nilpotent. For infinite-dimensional algebras nilpotency does not follow from the Engel property. However, a finitely-generated Lie algebra over a field of characteristic zero in which for some (not depending on ) is nilpotent (Zel'manov's theorem, cf. also [3]). For characteristic non-zero this is an open problem.

References

[1]	S. Lie, F. Engel, "Theorie der Transformationsgruppen" , 3 , Leipzig (1893)
[2]	W. Killing, "Die Zusammensetzung der stetigen endlichen Transformationsgruppen" Math. Ann. , 31 (1888) pp. 252–290
[3]	J. Levitzki, "On a problem of A. Kurosh" Bull. Amer. Math. Soc. , 52 (1946) pp. 1033–1035
[4]	N. Jacobson, "Lie algebras" , Interscience (1962) ((also: Dover, reprint, 1979))
[5]	N. Bourbaki, "Elements of mathematics. Lie groups and Lie algebras" , Addison-Wesley (1975) (Translated from French)