Engel theorem
Suppose that for a finite-dimensional Lie algebra 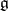 over a field
over a field 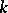 the linear operators
the linear operators
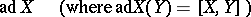 |
are nilpotent for all 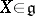 . Then there is a basis of
. Then there is a basis of 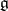 in which the matrices of all operators
in which the matrices of all operators 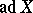 are triangular with zeros on the main diagonal.
are triangular with zeros on the main diagonal.
F. Engel proved (around 1887, published in [1]) that a Lie algebra 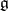 with this property is solvable, from which, by a theorem of S. Lie (cf. Lie theorem), the assertion stated above follows immediately. The first published proof of Engel's theorem is due to W. Killing [2], who acknowledges Engel's priority. Engel's theorem is often stated in the following more general form: If
with this property is solvable, from which, by a theorem of S. Lie (cf. Lie theorem), the assertion stated above follows immediately. The first published proof of Engel's theorem is due to W. Killing [2], who acknowledges Engel's priority. Engel's theorem is often stated in the following more general form: If 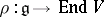 is a linear representation of a finite-dimensional Lie algebra
is a linear representation of a finite-dimensional Lie algebra 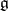 in a vector space
in a vector space 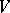 (where
(where 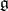 and
and 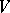 are regarded over an arbitrary field) and if
are regarded over an arbitrary field) and if 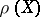 is a nilpotent endomorphism for any
is a nilpotent endomorphism for any 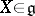 , then there is a non-zero vector
, then there is a non-zero vector 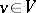 such that
such that 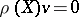 for any
for any 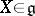 . If
. If  is finite-dimensional, this implies the existence of a basis in
is finite-dimensional, this implies the existence of a basis in 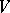 in which all the
in which all the 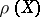 have triangular matrices with zeros on the main diagonal (or, what is the same, there is a complete flag
have triangular matrices with zeros on the main diagonal (or, what is the same, there is a complete flag 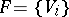 in
in 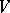 for which
for which 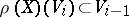 for all
for all 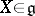 and
and 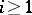 ). The conclusion of Engel's theorem is also true for any representation
). The conclusion of Engel's theorem is also true for any representation 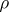 for which the Lie algebra
for which the Lie algebra 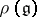 is the linear hull of a subset consisting of nilpotent endomorphisms and that is closed under the operation of commutation. A Lie algebra
is the linear hull of a subset consisting of nilpotent endomorphisms and that is closed under the operation of commutation. A Lie algebra 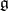 is called an Engel algebra if any
is called an Engel algebra if any 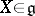 is an Engel element, that is, if all the operators
is an Engel element, that is, if all the operators 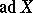 ,
, 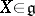 , are nilpotent or, what is the same, if for any
, are nilpotent or, what is the same, if for any  there is an
there is an  such that
such that
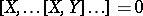 |
( brackets) for any
brackets) for any 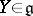 . A finite-dimensional Lie algebra is an Engel algebra if and only if it is nilpotent. For infinite-dimensional algebras nilpotency does not follow from the Engel property. However, a finitely-generated Lie algebra over a field of characteristic zero in which
. A finite-dimensional Lie algebra is an Engel algebra if and only if it is nilpotent. For infinite-dimensional algebras nilpotency does not follow from the Engel property. However, a finitely-generated Lie algebra over a field of characteristic zero in which 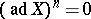 for some
for some  (not depending on
(not depending on 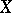 ) is nilpotent (Zel'manov's theorem, cf. also [3]). For characteristic non-zero this is an open problem.
) is nilpotent (Zel'manov's theorem, cf. also [3]). For characteristic non-zero this is an open problem.
References
| [1] | S. Lie, F. Engel, "Theorie der Transformationsgruppen" , 3 , Leipzig (1893) |
| [2] | W. Killing, "Die Zusammensetzung der stetigen endlichen Transformationsgruppen" Math. Ann. , 31 (1888) pp. 252–290 |
| [3] | J. Levitzki, "On a problem of A. Kurosh" Bull. Amer. Math. Soc. , 52 (1946) pp. 1033–1035 |
| [4] | N. Jacobson, "Lie algebras" , Interscience (1962) ((also: Dover, reprint, 1979)) |
| [5] | N. Bourbaki, "Elements of mathematics. Lie groups and Lie algebras" , Addison-Wesley (1975) (Translated from French) |
Engel theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Engel_theorem&oldid=16295