Elliptic geometry

A geometry in a space with a Riemannian curvature that is constant and positive in any two-dimensional direction. Elliptic geometry is a higher-dimensional generalization of the Riemann geometry.

Comments

Thus, elliptic geometry is the geometry of real projective space endowed with positive sectional curvature (i.e. the geometry of the sphere in with antipodal points, or antipodes, identified). An exposition of it is given in [a1], Chapt. 19; generalizations are given in [a2]. Some details follow.

Let be an -dimensional Euclidean space and the associated projective space of all straight lines through the origin. For let be the angle (in the Euclidean sense) between the lines and in . If and are two lines in intersecting in , then the angle between and 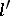is the angle in between the corresponding planes and in (which intersect in the line ). The space with this metric (and this notion of angle) is called the elliptic space associated with . It is of course closely related to the spherical geometry of , being in fact a quotient. The topology induced by the metric is the usual one.

Consider for the moment the spherical geometry of 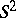, i.e. the lines are great circles. Take e.g. the equator. Then all lines in perpendicular to the equator meet in the North and South poles, the polar points of the equator. Identifying antipodal points one obtains , in which therefore for every line there is unique point point 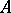, the (absolute) polar of through which every line perpendicular to 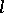passes. Conversely, to every point of there corresponds an (absolute) polar line.

This generalizes. Let 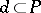be an -dimensional plane in 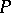, then the (absolute) polar of 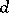in is the plane of dimension consisting of all points such that for all , . Thus, for the polar of a line is a line.

References

[a1]	M. Berger, "Geometry" , II , Springer (1987)
[a2]	H. Busemann, "Recent synthetic differential geometry" , Springer (1970)