Dynamic game

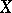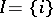A variant of a positional game distinguished by the fact that in such a game the players control the "motion of a point" in the state space . Let be the set of players. To each point 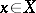corresponds a set 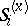of elementary strategies of player 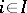at this point, and hence, also, the set 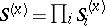of elementary situations at . The periodic distribution functions

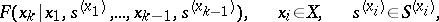representing the law of motion of the controlled point, which is known to all players, is defined on 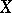. If 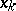is fixed, the function 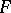is measurable with respect to all the remaining arguments. A sequence 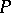of successive states and elementary situations is a play of a general dynamic game. It is inductively defined as follows: Let there be given a segment of the play (an opening) 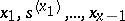(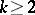), and let each player 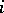choose his elementary strategy 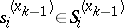so that the elementary situation 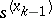arises; the game then continues, at random, in accordance with the distribution 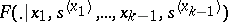, into the state 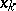. In each play 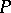the pay-off 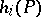of player 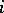is defined. If the set of all plays is denoted by 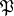, the dynamic game is specified by the system

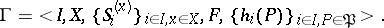In a dynamic game it is usually assumed that, at the successive moments of selection of an elementary strategy, the players know the preceding opening. In such a case a pure strategy of player 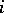is a selection of functions 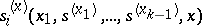which put the opening ending in into correspondence with the elementary strategy 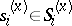. Dynamic games in which the preceding opening is only known partly to the players — e.g. games with "information lag" — have also been studied.

For a game to be specified, each situation must induce a probability measure 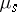on the set of all plays, and the mathematical expectation 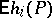with respect to the measure 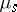must exist. This mathematical expectation is also the pay-off of player 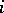in situation .

In general, the functions 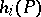are arbitrary, but the most frequently studied dynamic games are those with terminal pay-off (the game is terminated as soon as 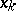appears in a terminal set 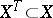, and 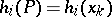where 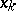is the last situation in the game), and those with integral pay-off ().

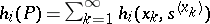Dynamic games are regarded as the game-like variant of a problem of optimal control with discrete time. It is in fact reduced to such a problem if the number of players is one. If, in a dynamic game, 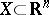, continuous time is substituted for discrete time and the random factors are eliminated, a differential game is obtained, which may thus be regarded as a variant of a dynamic game (see also Differential games).

Stochastic games, recursive games and survival games are special classes of dynamic games (cf. also Stochastic game; Recursive game; Game of survival).

References

[1]	N.N. Vorob'ev, "The present state of the theory of games" Russian Math. Surveys , 25 : 2 (1970) pp. 77–136 Uspekhi Mat. Nauk , 25 : 2 (1970) pp. 81–140