Double limit
The double limit of a sequence, the limit of a double sequence,  ,
, 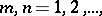 is a number
is a number  which is defined as follows: For any
which is defined as follows: For any 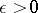 there exists an
there exists an  such that for all
such that for all 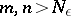 the equality
the equality
 |
is valid. The notation is
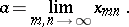 |
If for any 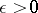 there is an
there is an 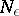 such that for all
such that for all 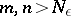 the inequality
the inequality 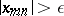 is fulfilled, then the sequence
is fulfilled, then the sequence 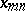 has infinity as its limit:
has infinity as its limit:
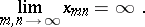 |
The infinite limits
 |
are defined in the same manner. The double limit of a sequence is a special case of the double limit of a function over a set, namely when this set consists of the points on the plane with integer coordinates 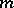 and
and  . Accordingly, the double limit of a sequence is connected with its repeated limits as in the general case.
. Accordingly, the double limit of a sequence is connected with its repeated limits as in the general case.
The double limit of a function is the limit of a function of two variables, defined as follows. Let the function  be defined on a set
be defined on a set 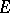 in the
in the 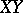 -plane, and let
-plane, and let  be a limit point of it (cf. Limit point of a set). A number
be a limit point of it (cf. Limit point of a set). A number  is said to be the double limit of the function
is said to be the double limit of the function 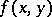 at the point
at the point  , or as
, or as 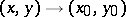 , if for any
, if for any 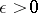 there exists a
there exists a 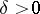 such that for all the points
such that for all the points 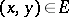 the coordinates of which satisfy the inequalities
the coordinates of which satisfy the inequalities
 |
the inequality
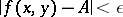 |
is valid. In such a case the limit is written as
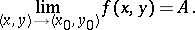 |
The double limit of a function may be formulated in terms of the limit of a sequence:
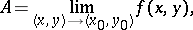 |
if for any sequence
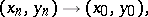 |
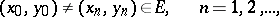 |
the condition
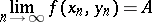 |
is satisfied. The double limit of a function as its arguments tend to infinity, as well as the definitions of infinite double limits of a function, are formulated in a similar manner. There exists a connection between the double limit of a function and the repeated limit of a function at a point 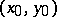 or at
or at 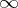 : Let
: Let 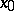 and
and  be limit points (finite or infinite) of the real subsets
be limit points (finite or infinite) of the real subsets  and
and 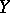 , and let
, and let  . If for a function a finite or infinite double limit
. If for a function a finite or infinite double limit
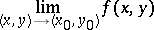 |
exists, and if for any 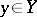 there is a finite limit
there is a finite limit
 |
then the repeated limit
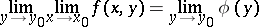 |
exists and is equal to the double limit of the function.
Using the concept of a neighbourhood, the following form may be assigned to the definition of the double limit of a function: Let  be a limit point
be a limit point  of a set
of a set 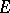 or the symbol
or the symbol 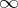 , the set
, the set 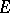 being unbounded in the latter case, and let
being unbounded in the latter case, and let 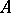 be a number or one of the symbols
be a number or one of the symbols 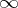 ,
, 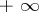 ,
, 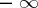 . Then
. Then
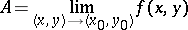 |
if for any neighbourhood  of the point or symbol
of the point or symbol 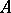 there exists a neighbourhood
there exists a neighbourhood 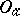 of the number or symbol
of the number or symbol  such that for all
such that for all 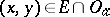 ,
, 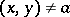 , the condition
, the condition  is satisfied. In this form the definition of the double limit of a function is applied to the case when the function
is satisfied. In this form the definition of the double limit of a function is applied to the case when the function 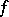 is defined on the product of two topological spaces
is defined on the product of two topological spaces  and
and 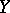 and
and 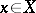 ,
, 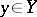 , while the values of
, while the values of 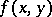 also belong to a topological space.
also belong to a topological space.
Double limit. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Double_limit&oldid=46770