Dirichlet box principle

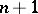A theorem according to which any sample of sets containing in total more than elements comprises at least one set with at least two elements. Dirichlet's box principle can be formulated in a most popular manner as follows: If "boxes" contain "objects" , then at least one "box" contains at least two "objects" . The principle is frequently used in the theory of Diophantine approximations and in the theory of transcendental numbers to prove that a system of linear inequalities can be solved in integers (cf. Dirichlet theorem in the theory of Diophantine approximations).