Differential operator on a module
A mapping of modules over a commutative ring which is an analogue of the concept of a differential operator. Let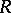 
be a commutative ring, let 
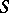be a subring of 
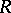and let 
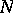and 
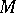be two 
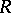-modules. A homomorphism of 
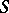-modules 
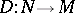is said to be a differential operator of order 
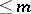, where 
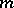is a non-negative integer, if for any 
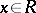the mapping 
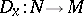defined by the formula
 |
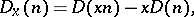is a differential operator of order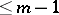 
. A differential operator of order zero is a homomorphism of 
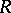-modules 
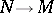. The set of all differential operators of order 
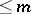forms a submodule 
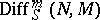of the 
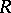-module of all homomorphisms of 
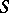-modules 
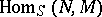. In particular,
 |
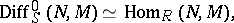and the quotient module
 |
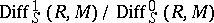is isomorphic to the module of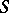 
-derivations 
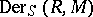of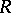 
with values in 
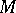. The union 
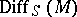of the increasing family of submodules
 |
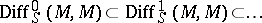is a filtered associative ring with respect to the operation of composition of mappings. This ring is known as the ring of differential operators of the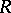 
-module 
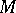over the subring 
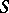, while the corresponding graded ring
 |
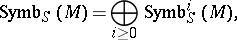where
 |
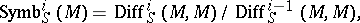is said to be the module of symbols. The image of a differential operator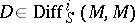 
in the ring 
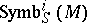is said to be the symbol of the differential operator.
If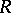 
is an algebra over the field of rational numbers and the module of differentials 
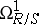is projective, then there exists an isomorphism between the 
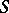-algebra 
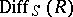and the enveloping algebra of the Lie algebra of 
-derivations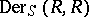 
. In this case the ring 
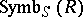is isomorphic to the symmetric algebra of the 
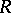-module 
.
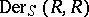For example, let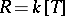 
be the ring of polynomials over a field 
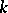; the mappings 
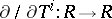, defined by the formula
 |
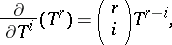are differential operators of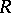 
over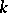 
of order 
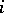. The ring of differential operators 
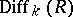is a free module over 
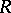with basis 
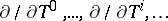. Multiplication is given by the formula
 |
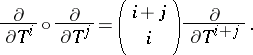In particular,
 |
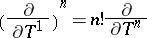(Taylor's formula) which, if the characteristic of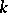 
is equal to zero, yields
 |
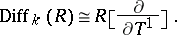If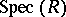 
is an affine group 
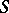-scheme, invariant differential operators of 
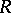may also be considered [2].
References
| [1] | A.M. Vinogradov, I.S. Krasil'shchikov, "What is the Hamilton formalism?" Russian Math. Surveys , 30 : 1 (1975) pp. 177–202 Uspekhi Mat. Nauk. , 30 : 1 (1975) pp. 173–198 |
| [2] | A. Grothendieck, "Eléments de géométrie algébrique. IV Etude locale des schémas et des morphisms des schémas I" Publ. Math. IHES , 20 (1960) |
| [3] | M. Demazure, P. Gabriel, "Groupes algébriques" , 1 , Masson (1970) |
| [4] | J.E. Björk, "The global homological dimension of some algebras of differential operators" Invent. Math. , 17 : 1 (1972) pp. 67–78 |
Differential operator on a module. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Differential_operator_on_a_module&oldid=46695