Differential comitant
A differentiable mapping 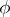 of a tensor bundle
of a tensor bundle 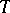 on a manifold
on a manifold 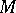 into a tensor bundle
into a tensor bundle 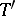 on the same manifold such that if
on the same manifold such that if  and
and  are the projections of
are the projections of 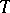 and
and 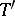 on
on  , then
, then
 |
The components of the tensor 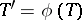 in a local chart
in a local chart 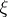 on
on  depend on
depend on 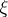 only by means of the components of the tensor
only by means of the components of the tensor 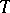 .
.
In particular, when 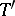 is reduced to the bundle of relative scalars of weight
is reduced to the bundle of relative scalars of weight 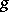 , the differential comitant is a differential invariant of weight
, the differential comitant is a differential invariant of weight 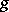 .
.
Comments
Thus, a differential comitant is simply a vector bundle mapping from the tensor bundle 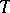 to the tensor bundle
to the tensor bundle 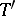 .
.
The bundle of relative scalars of weight 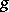 is constructed as follows. It is a line bundle. Let
is constructed as follows. It is a line bundle. Let  be an atlas for the manifold
be an atlas for the manifold  with coordinate change diffeomorphisms
with coordinate change diffeomorphisms 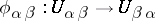 . Take the trivial line bundles
. Take the trivial line bundles 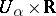 over each
over each 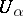 and glue them together by means of the diffeomorphisms
and glue them together by means of the diffeomorphisms 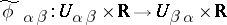 ,
,  , where
, where 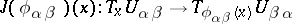 is the Jacobian matrix of
is the Jacobian matrix of  at
at  .
.
Cf. also Differential invariant. Note however that for differential invariants not only tensor bundles but also (tensor and exterior products of) higher jet bundles and their duals are considered.
Differential comitant. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Differential_comitant&oldid=46664