Diagonal product of mappings

,

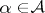
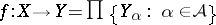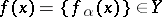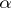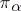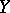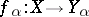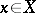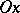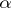The mapping defined by the equation . The diagonal product of mappings satisfies, for any , the relation , where denotes the projection of the product on the factor . The diagonal product of continuous mappings is continuous. A family of mappings of topological spaces is said to be partitioning if for any point and neighbourhood of there exist an index and an open subset such that . If 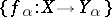is a partitioning family of mappings and if 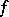is the diagonal product of the mappings 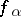, then 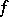is an imbedding of 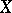into the product 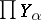, i.e. 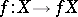is a homeomorphism. The diagonal product of mappings was used by A.N. Tikhonov to imbed a completely-regular space of weight in the cube .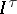

Comments

Instead of calling a family of mappings partitioning, one says that it separates points and closed sets.

In an arbitrary category with products, cf. Direct product, the diagonal product of mappings is given by the universal property defining the direct product. Indeed, categorically the product is an object together with morphisms: 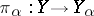such that for every family of morphisms 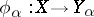there is a unique morphism 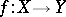such that .

Tikhonov's imbedding result is in [a2]. E. Čech, inspired by Tikhonov's result, obtained the following imbedding theorem [a1]: Let be the family of continuous mappings from a completely-regular space into the unit interval 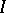. Then the diagonal mapping is an imbedding, and the closure of 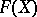in is equivalent to the Stone–Čech compactification of .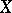

References

[a1]	E. Čech, "On bicompact spaces" Ann. of Math. , 38 (1937) pp. 823–844
[a2]	A.N. [A.N. Tikhonov] Tichonoff, "Ueber die topologische Erweiterung von Räumen" Math. Ann. , 102 (1929) pp. 544–561