Diagonal operator
An operator 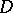 defined on the (closed) linear span of a basis
defined on the (closed) linear span of a basis 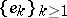 in a normed (or only locally convex) space
in a normed (or only locally convex) space  by the equations
by the equations 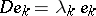 , where
, where 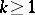 and where
and where 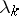 are complex numbers. If
are complex numbers. If  is a continuous operator, one has
is a continuous operator, one has
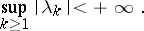 |
If 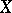 is a Banach space, this condition is equivalent to the continuity of
is a Banach space, this condition is equivalent to the continuity of 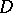 if and only if
if and only if 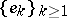 is an unconditional basis in
is an unconditional basis in 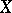 . If
. If 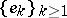 is an orthonormal basis in a Hilbert space
is an orthonormal basis in a Hilbert space 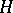 , then
, then 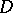 is a normal operator, and
is a normal operator, and 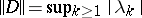 , while the spectrum of
, while the spectrum of 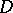 coincides with the closure of the set
coincides with the closure of the set 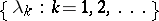 . A normal and completely-continuous operator
. A normal and completely-continuous operator 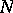 is a diagonal operator in the basis of its own eigen vectors; the restriction of a diagonal operator (even if it is normal) to its invariant subspace need not be a diagonal operator; given an
is a diagonal operator in the basis of its own eigen vectors; the restriction of a diagonal operator (even if it is normal) to its invariant subspace need not be a diagonal operator; given an 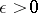 , any normal operator
, any normal operator 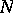 on a separable space
on a separable space 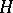 can be represented as
can be represented as 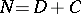 , where
, where 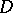 is a diagonal operator,
is a diagonal operator, 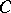 is a completely-continuous operator and
is a completely-continuous operator and 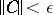 .
.
A diagonal operator in the broad sense of the word is an operator 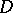 of multiplication by a complex function
of multiplication by a complex function 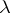 in the direct integral of Hilbert spaces
in the direct integral of Hilbert spaces
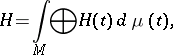 |
i.e.
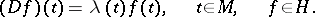 |
References
| [1] | I.M. Singer, "Bases in Banach spaces" , 1 , Springer (1970) |
| [2] | J. Wermer, "On invariant subspaces of normal operators" Proc. Amer. Math. Soc. , 3 : 2 (1952) pp. 270–277 |
| [3] | I.D. Berg, "An extension of the Weyl–von Neumann theorem to normal operators" Trans. Amer. Math. Soc. , 160 (1971) pp. 365–371 |
Comments
For the notion of an unconditional basis see Basis.
For diagonal operators in the broad sense (and the corresponding notion of a diagonal algebra) see [a1].
References
| [a1] | M. Takesaki, "Theory of operator algebras" , 1 , Springer (1979) pp. 259, 273 |
| [a2] | P.R. Halmos, "A Hilbert space problem book" , Springer (1982) |
Diagonal operator. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Diagonal_operator&oldid=46640