Density hypothesis

A proposed inequality providing a bound for the number 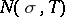of zeros 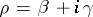of the Riemann zeta-function

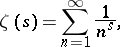where 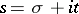, in the rectangle , .

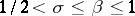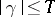The most exact formulation of the density hypothesis is

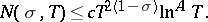A simpler, but less accurate, form of the density hypothesis is

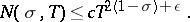The density hypothesis enables one to obtain results in the theory of prime numbers that are comparable with those following from the Riemann hypothesis. For example, it follows from the density hypothesis that for sufficiently large there is at least one prime number in each segment .

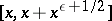The density hypothesis is a consequence of the stronger Lindelöf hypothesis. A difference from the latter is that the density hypothesis has been partially proved, in terms of various density theorems, beginning with certain values .

For the number 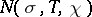of zeros of Dirichlet 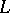-functions

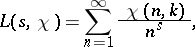where 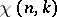is a character modulo 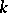, an analogous density hypothesis is posed. In averaged form, this is

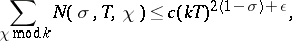(1)

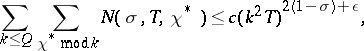(2)

where 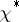is a primitive character modulo .

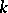The density hypothesis for Dirichlet 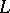functions is used in the theory of the distribution of prime numbers belonging to arithmetic progressions.

References

[1]	H. Davenport, "Multiplicative number theory" , Springer (1980)
[2]	A.F. Lavrik, "A survey of Linnik's large sieve and the density theory of zeros of 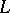-functions" Russian Math. Surveys , 35 : 2 (1980) pp. 63–76 Uspekhi Mat. Nauk , 35 : 2 (1980) pp. 55–65

Comments

For extra references see also Density method. Cf. also Distribution of prime numbers.

Let 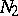be the double sum in (2) above. Then the estimates of A.I. Vinogradov [a1], [a2] and E. Bombieri [a3] (the Bombieri–Vinogradov theorem) are, respectively,

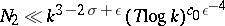and

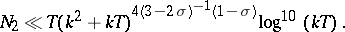Let 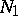be the sum in (1) above. More recent results on 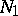and 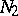for, respectively, 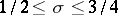, 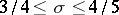and 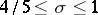are due to H.L. Montgomery, M.N. Huxley, and M. Jutila and are, respectively (cf. [2]),

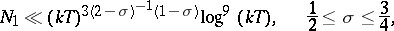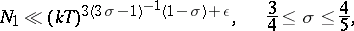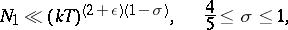and for ,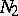

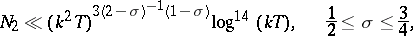References

[a1]	A.I. Vinogradov, "The density hypothesis for Dirichlet 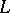-series" Izv. Akad. Nauk SSSR Ser. Mat. , 29 (1965) pp. 903–934 (In Russian)
[a2]	A.I. Vinogradov, "Correction to "The density hypothesis for Dirichlet L-series" " Izv. Akad. Nauk SSSR Ser. Mat. , 30 (1966) pp. 719–720 (In Russian)
[a3]	E. Bombieri, "On the large sieve" Mathematika , 12 (1965) pp. 201–225