Correlation
duality
A bijective mapping 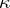 between projective spaces of the same finite dimension such that
between projective spaces of the same finite dimension such that 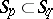 implies
implies 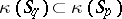 . The image of a sum of subspaces under a correlation is the intersection of their images and, conversely, the image of an intersection is the sum of the images. In particular, the image of a point is a hyperplane and vice versa. A necessary and sufficient condition for the existence of a correlation of a projective space
. The image of a sum of subspaces under a correlation is the intersection of their images and, conversely, the image of an intersection is the sum of the images. In particular, the image of a point is a hyperplane and vice versa. A necessary and sufficient condition for the existence of a correlation of a projective space 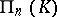 over a division ring
over a division ring 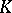 onto a space
onto a space 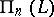 over a division ring
over a division ring 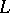 is that there exists an anti-isomorphism
is that there exists an anti-isomorphism 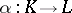 , i.e. a bijective mapping for which
, i.e. a bijective mapping for which 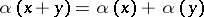 ,
, 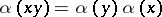 ; in that case
; in that case 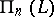 is dual to
is dual to 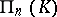 . Examples of spaces with an auto-correlation, i.e. a correlation onto itself, are the real projective spaces
. Examples of spaces with an auto-correlation, i.e. a correlation onto itself, are the real projective spaces 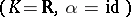 , the complex projective spaces
, the complex projective spaces 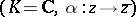 and the quaternion projective spaces
and the quaternion projective spaces 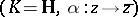 .
.
A polarity is an auto-correlation 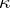 satisfying
satisfying 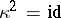 . A projective space
. A projective space 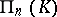 over a division ring
over a division ring 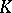 admits a polarity if and only if
admits a polarity if and only if 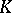 admits an involutory anti-automorphism, i.e. an anti-automorphism
admits an involutory anti-automorphism, i.e. an anti-automorphism 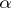 with
with 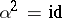 .
.
A subspace 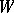 is called a null subspace relative to an auto-correlation
is called a null subspace relative to an auto-correlation 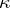 if
if 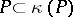 for any point
for any point 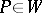 , and strictly isotropic if
, and strictly isotropic if 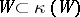 . Any strictly isotropic subspace is a null subspace. A polarity relative to which the whole space is a null space is called a null (or symplectic) polarity (see also Polarity).
. Any strictly isotropic subspace is a null subspace. A polarity relative to which the whole space is a null space is called a null (or symplectic) polarity (see also Polarity).
Let the projective space 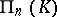 over a division ring
over a division ring 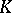 be interpreted as the set of linear subspaces of the (left) linear space
be interpreted as the set of linear subspaces of the (left) linear space 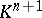 over
over 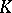 . A semi-bilinear form on
. A semi-bilinear form on 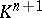 is a mapping
is a mapping 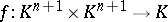 together with an anti-automorphism
together with an anti-automorphism 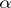 of
of 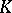 such that
such that
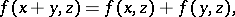 |
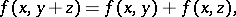 |
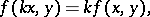 |
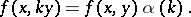 |
In particular, if 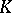 is a field and
is a field and 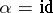 , then
, then 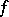 is a bilinear form. A semi-bilinear form
is a bilinear form. A semi-bilinear form 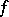 is called non-degenerate provided
is called non-degenerate provided 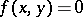 for all
for all  (all
(all 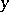 ) implies
) implies 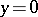 (
(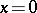 , respectively). Any auto-correlation
, respectively). Any auto-correlation 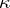 of
of 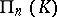 can be represented with the aid of a non-degenerate semi-bilinear form
can be represented with the aid of a non-degenerate semi-bilinear form 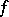 in the following way: for a subspace
in the following way: for a subspace 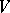 of
of 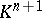 its image is the orthogonal complement of
its image is the orthogonal complement of 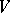 with respect to
with respect to 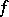 :
:
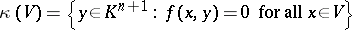 |
(the Birkhoff–von Neumann theorem, ). 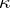 is a polarity if and only if
is a polarity if and only if  is reflexive, i.e. if
is reflexive, i.e. if 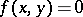 implies
implies 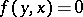 . By multiplying
. By multiplying 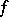 by a suitable element of
by a suitable element of 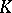 one can bring any reflexive non-degenerate semi-bilinear form
one can bring any reflexive non-degenerate semi-bilinear form 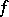 and the corresponding automorphism
and the corresponding automorphism 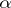 in either of the following two forms:
in either of the following two forms:
1) 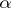 is an involution, i.e.
is an involution, i.e. 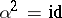 , and
, and
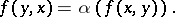 |
In this case one calls 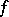 symmetric if
symmetric if 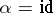 (and hence necessarily
(and hence necessarily 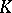 is a field) and Hermitian if
is a field) and Hermitian if 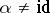 .
.
2) 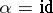 (and hence
(and hence 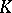 is a field) and
is a field) and
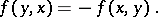 |
Such an 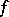 is called anti-symmetric.
is called anti-symmetric.
A special example of a correlation is the following. Let 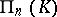 be a projective space over a division ring
be a projective space over a division ring 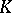 . Define the opposite division ring
. Define the opposite division ring 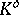 as the set of elements of
as the set of elements of 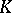 with the same addition but with multiplication
with the same addition but with multiplication
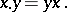 |
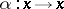 is an anti-isomorphism from
is an anti-isomorphism from 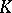 onto
onto 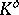 which defines the canonical correlation from
which defines the canonical correlation from 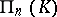 onto
onto 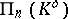 . The (left) projective space
. The (left) projective space 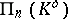 , which can be identified with the right projective space
, which can be identified with the right projective space 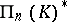 , i.e. with the set of linear subspaces of the
, i.e. with the set of linear subspaces of the 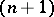 -dimensional right vector space
-dimensional right vector space 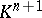 , is the (canonical) dual space of
, is the (canonical) dual space of 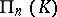 (cf. Projective algebra, the construction of
(cf. Projective algebra, the construction of 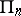 ).
).
Comments
References
| [a1] | R. Baer, "Linear algebra and projective geometry" , Acad. Press (1952) |
| [a2] | G. Birkhoff, J. von Neumann, "The logic of quantum mechanics" Ann. of Math. , 37 (1936) pp. 823–843 |
| [a3] | J.A. Dieudonné, "La géométrie des groups classiques" , Springer (1963) |
| [a4] | D.R. Hughes, F.C. Piper, "Projective planes" , Springer (1972) |
Correlation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Correlation&oldid=46520