Complex
A set 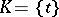 of elements
of elements 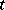 that is partially ordered by a reflexive regular transitive relation
that is partially ordered by a reflexive regular transitive relation  , together with an integer-valued function
, together with an integer-valued function 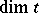 , called the dimension of the element
, called the dimension of the element 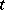 , and a number
, and a number 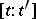 , called the incidence coefficient of the elements
, called the incidence coefficient of the elements 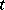 and
and 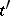 , satisfying the conditions: 1)
, satisfying the conditions: 1) 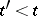 implies
implies 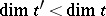 ; 2)
; 2) 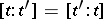 ; 3)
; 3) 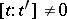 implies that either
implies that either 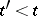 or
or 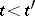 , and that
, and that 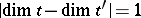 ; and 4) for any pair of elements
; and 4) for any pair of elements 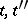 in
in 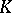 the dimensions of which differ by two, there exists in
the dimensions of which differ by two, there exists in 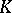 at most a finite number of elements
at most a finite number of elements 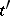 such that
such that
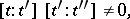 |
and, moreover,
 |
On replacing 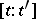 by
by 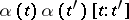 , where
, where 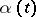 is a function with values
is a function with values 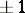 , one obtains a complex that can be identified with
, one obtains a complex that can be identified with 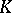 ; in other words, the incidences
; in other words, the incidences 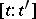 are determined up to factors
are determined up to factors 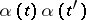 ; transition from one value to the other is called a change of orientation of the complex
; transition from one value to the other is called a change of orientation of the complex 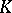 ; the element
; the element  preserves or changes its orientation according to whether
preserves or changes its orientation according to whether 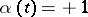 or
or 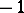 , respectively.
, respectively.
A complex 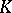 is called finite dimensional, more precisely,
is called finite dimensional, more precisely,  -dimensional, if
-dimensional, if  is the maximum dimension of the elements in
is the maximum dimension of the elements in 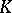 ; if there is no element of the maximum dimension
; if there is no element of the maximum dimension  , then
, then 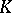 is called infinite dimensional. The star of an element
is called infinite dimensional. The star of an element 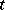 in the complex
in the complex 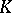 is the set of all elements
is the set of all elements 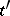 in
in 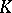 such that
such that 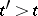 . The closure of an element
. The closure of an element 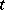 in
in 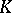 is the set of all elements
is the set of all elements 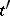 in
in 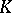 such that
such that  . The boundary of an element
. The boundary of an element 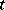 in
in 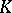 is the set of all elements
is the set of all elements 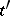 in
in 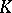 such that
such that 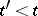 and
and 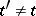 . An element
. An element 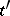 is called a face of an element
is called a face of an element  in
in 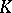 if
if 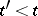 ; a face
; a face  of
of 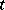 is called a proper face if
is called a proper face if 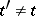 . Two elements
. Two elements 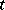 and
and 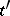 in
in 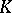 are said to be incident if
are said to be incident if 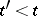 or
or 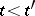 . A complex
. A complex 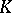 is called finite if the set of its elements is finite. A complex
is called finite if the set of its elements is finite. A complex  is called star-finite (respectively, closure-finite) if the star (respectively, the closure) of each of its elements consists of a finite number of elements. A complex is said to be locally finite if it is star-finite and closure-finite.
is called star-finite (respectively, closure-finite) if the star (respectively, the closure) of each of its elements consists of a finite number of elements. A complex is said to be locally finite if it is star-finite and closure-finite.
A subcomplex of a complex 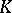 is any subset of
is any subset of  that is a complex under the same dimensions and incidence coefficients as
that is a complex under the same dimensions and incidence coefficients as 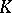 . A subcomplex is closed closed if it contains the closure of each of its elements, and open if it contains the star of each of its elements. The complement of a closed complex is an open complex, and conversely. The star of each element of any complex is an open subcomplex, while the closure and boundary are closed subcomplexes. The
. A subcomplex is closed closed if it contains the closure of each of its elements, and open if it contains the star of each of its elements. The complement of a closed complex is an open complex, and conversely. The star of each element of any complex is an open subcomplex, while the closure and boundary are closed subcomplexes. The  -dimensional skeleton, or
-dimensional skeleton, or  -skeleton,
-skeleton, 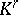 of a complex
of a complex  is the set of all elements
is the set of all elements 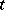 in
in 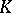 for which
for which 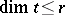 ; it is a closed subcomplex.
; it is a closed subcomplex.
Two complexes 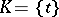 and
and 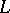 are said to be isomorphic if there is a bijective mapping
are said to be isomorphic if there is a bijective mapping 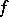 of the set
of the set 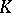 to the set
to the set 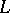 such that
such that 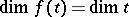 and
and 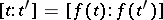 .
.
The most important type of complex is a simplicial complex, of which there exist two kinds: an abstract complex and a geometric complex.
An abstract simplicial complex 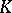 has for its elements abstract simplices (simplexes) of different dimensions. An
has for its elements abstract simplices (simplexes) of different dimensions. An  -dimensional simplex
-dimensional simplex 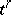 is a set of
is a set of 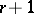 objects
objects  . These objects, that is, the
. These objects, that is, the  -dimensional simplices, are called the vertices of the complex
-dimensional simplices, are called the vertices of the complex 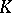 . A simplex is oriented if its vertex set is ordered, where orderings that differ by an even permutation determine the same orientation. The
. A simplex is oriented if its vertex set is ordered, where orderings that differ by an even permutation determine the same orientation. The  -dimensional faces of a simplex
-dimensional faces of a simplex 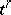 are the
are the  -dimensional simplices the vertices of which are contained among those of
-dimensional simplices the vertices of which are contained among those of 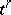 . A simplicial complex
. A simplicial complex  contains all faces of each of its simplices. The relation
contains all faces of each of its simplices. The relation 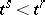 means that
means that 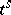 is a face of
is a face of 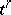 . The faces
. The faces 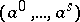 and
and 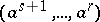 are called opposite faces of the simplex
are called opposite faces of the simplex 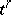 . If
. If 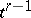 is the face of
is the face of 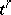 opposite to the vertex
opposite to the vertex 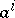 , then
, then
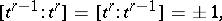 |
according to whether 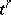 has the same orientation as
has the same orientation as 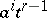 or not. If
or not. If 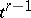 is not a face of
is not a face of 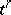 , then
, then
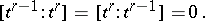 |
By giving an orientation to each simplex of a simplicial complex one obtains an oriented complex 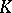 .
.
An abstract simplicial complex is defined if the set of its vertices is known as well as the system, called a scheme, of all those finite subsets of this set that are to be taken as the simplices; here it is required that each vertex belongs to at least one element of the system and that each subset of an element belonging to the system also belongs to the system. Dimension, orientation, etc., are defined as before.
A polyhedral (cellular) complex of an  -dimensional Euclidean space
-dimensional Euclidean space 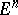 is a countable locally finite complex
is a countable locally finite complex 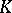 the elements of which are
the elements of which are  -dimensional cells
-dimensional cells 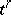 , i.e. bounded convex open subsets of some
, i.e. bounded convex open subsets of some 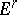 in
in 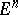 ,
,  , where the cells are pairwise disjoint, the union of the cells belonging to the closure of the element
, where the cells are pairwise disjoint, the union of the cells belonging to the closure of the element 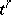 is the topological closure
is the topological closure  of
of 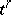 in
in 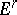 , and the topological closure of the union of the cells not belonging to the star of
, and the topological closure of the union of the cells not belonging to the star of 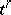 does not intersect
does not intersect 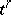 . Here
. Here 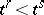 means that either
means that either 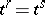 or
or  , and
, and 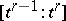 is defined by the incidence coefficients
is defined by the incidence coefficients 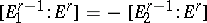 , where
, where 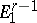 and
and  are the two regions into which the space
are the two regions into which the space 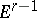 containing
containing 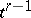 divides
divides 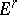 . The union of the cells of the polyhedral complex
. The union of the cells of the polyhedral complex 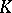 obtained in this manner with the topology induced from
obtained in this manner with the topology induced from 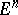 is called a polyhedron and is usually denoted by
is called a polyhedron and is usually denoted by 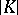 . A special form of a polyhedral complex is a Euclidean geometric simplicial complex, the elements of which are Euclidean simplices in
. A special form of a polyhedral complex is a Euclidean geometric simplicial complex, the elements of which are Euclidean simplices in 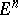 . An
. An  -dimensional Euclidean simplex
-dimensional Euclidean simplex 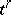 consists of points
consists of points 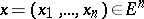 , defined by the relations
, defined by the relations
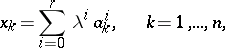 |
where 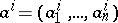 ,
, 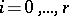 , are independent points of
, are independent points of 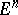 (i.e. they are not contained in any
(i.e. they are not contained in any 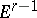 of
of 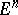 ),
), 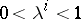 ,
,
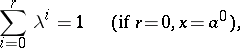 |
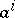 are called the vertices of
are called the vertices of 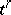 ,
, 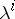 are the barycentric coordinates of the point
are the barycentric coordinates of the point  , and
, and 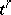 is called the geometric simplex formed by the abstract simplex
is called the geometric simplex formed by the abstract simplex 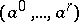 .
.
Let 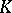 be a countable locally finite abstract simplicial complex with vertices in
be a countable locally finite abstract simplicial complex with vertices in 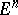 , where any vertices forming a simplex are independent, any two simplexes of
, where any vertices forming a simplex are independent, any two simplexes of 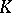 having no vertices in common generate disjoint geometric complexes, and the closure of the union of all those geometric simplices that are generated by simplices of
having no vertices in common generate disjoint geometric complexes, and the closure of the union of all those geometric simplices that are generated by simplices of 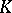 and which do not belong to some generated simplex does not intersect the latter. The notions of dimension, order, incidence, etc., are carried over from
and which do not belong to some generated simplex does not intersect the latter. The notions of dimension, order, incidence, etc., are carried over from  to the set of generated geometric simplices; this turns this set into a polyhedral complex, called a Euclidean realization of
to the set of generated geometric simplices; this turns this set into a polyhedral complex, called a Euclidean realization of 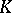 .
.
A geometric realization, not necessarily Euclidean, is also possible for any abstract simplicial complex. Let 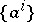 be the family of vertices of an arbitrary abstract simplicial complex
be the family of vertices of an arbitrary abstract simplicial complex  labelled by indices
labelled by indices 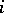 in a totally well-ordered set
in a totally well-ordered set 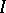 , let
, let 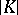 be the set of all systems
be the set of all systems 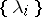 ,
, 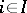 , of non-negative real numbers
, of non-negative real numbers 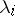 such that the vertices corresponding to non-zero coordinates
such that the vertices corresponding to non-zero coordinates 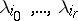 of the system
of the system 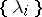 form a simplex
form a simplex  in
in 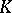 (the number of such coordinates is finite), and let
(the number of such coordinates is finite), and let 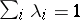 . The simplex
. The simplex 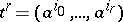 in
in 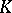 is put in correspondence with the set
is put in correspondence with the set  of all systems
of all systems 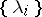 such that
such that 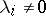 if and only if
if and only if 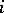 is one of the
is one of the 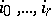 ; then
; then 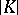 is the union of the sets
is the union of the sets 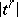 . Let
. Let 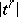 be homeomorphically imbedded in
be homeomorphically imbedded in 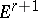 : Corresponding to the point
: Corresponding to the point 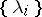 in
in 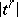 is the point
is the point 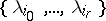 in
in 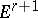 . This introduces a topology in
. This introduces a topology in 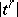 and in
and in 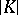 : A set in
: A set in 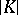 is taken to be open if its intersection with each
is taken to be open if its intersection with each 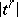 is open in
is open in  . The polyhedron
. The polyhedron 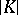 is called a geometric realization of the complex
is called a geometric realization of the complex 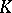 , and
, and  is called a triangulation of the polyhedron
is called a triangulation of the polyhedron 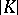 . A simplicial complex
. A simplicial complex 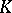 is finite (respectively, locally finite) if and only if
is finite (respectively, locally finite) if and only if 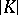 is a compact (respectively, locally compact) space. Local finiteness of a simplicial complex
is a compact (respectively, locally compact) space. Local finiteness of a simplicial complex 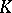 is also a necessary and sufficient condition for the metrizability of
is also a necessary and sufficient condition for the metrizability of 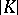 , where the metric is defined by the formula
, where the metric is defined by the formula
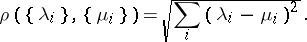 |
If 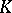 is a countable locally finite
is a countable locally finite  -dimensional complex, then it can be realized in the
-dimensional complex, then it can be realized in the 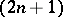 -dimensional Euclidean space
-dimensional Euclidean space 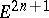 . A complex
. A complex 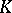 is realizable in a Hilbert space if
is realizable in a Hilbert space if  can be homeomorphically imbedded in this space such that every closed simplex in
can be homeomorphically imbedded in this space such that every closed simplex in 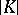 has a Euclidean realization; this is possible if and only if
has a Euclidean realization; this is possible if and only if 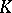 is a countable locally finite simplicial complex.
is a countable locally finite simplicial complex.
A finite geometric complex is a set of open geometric simplices that contains all the faces of each of the simplices and is such that the intersection of different simplices is empty. When studying closed simplices the second condition is replaced by the requirement that the intersection of two closed simplices be empty or a closed face of these simplices.
The notion of a complex finds its greatest application in homology theory. The use of simplicial complexes in the calculation of topological invariants of polyhedra is complicated by the fact that under triangulation of a polyhedron one may have to use many simplices. In this respect the CW-complex is preferable: in the latter the number of cells can be considerably fewer than the number of simplices in an arbitrary simplicial subdivision of the polyhedron. On the other hand, the simplicial complexes and triangulations have their advantages too. For example, in the simplicial approximation of a continuous mapping, in the composition and application of incidence matrices, in the use of complexes for the homological investigation of general topological spaces, etc.
A simplicial mapping from a complex 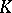 to a complex
to a complex 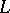 is a function
is a function 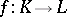 that sets up a correspondence between each vertex
that sets up a correspondence between each vertex  of
of 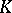 and a vertex
and a vertex 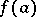 of
of 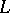 , such that whenever some vertices
, such that whenever some vertices  of
of 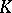 form a simplex in
form a simplex in 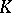 , then the vertices
, then the vertices  , some of which may be coincident, must also form simplex in
, some of which may be coincident, must also form simplex in 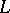 . The function
. The function 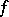 associates with each simplex
associates with each simplex 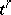 of
of 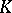 a simplex
a simplex 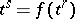 of
of 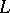 . A simplicial mapping
. A simplicial mapping 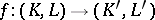 of a pair
of a pair 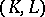 into a pair
into a pair 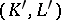 , where
, where 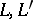 are closed subcomplexes of
are closed subcomplexes of 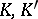 , respectively, is a simplicial mapping
, respectively, is a simplicial mapping 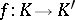 such that
such that 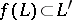 . The set of all simplicial complexes and their simplicial mappings forms a category, as does the set of all simplicial pairs and all their simplicial mappings.
. The set of all simplicial complexes and their simplicial mappings forms a category, as does the set of all simplicial pairs and all their simplicial mappings.
The homology of a complex, which, to begin with, was expressed by numerical invariants, subsequently came to be represented by algebraic means such as groups, modules, sheaves, etc. The scheme of their construction is as follows. Let 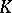 be an arbitrary complex and let
be an arbitrary complex and let 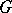 be an Abelian group; an
be an Abelian group; an  -dimensional chain complex (generally infinite)
-dimensional chain complex (generally infinite) 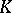 over the group of coefficients
over the group of coefficients 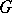 is a function
is a function 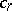 with domain the set of all
with domain the set of all  -dimensional elements of
-dimensional elements of 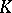 and with range
and with range 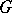 . The collection
. The collection 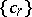 of all
of all  -dimensional chains
-dimensional chains 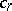 of the complex
of the complex 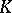 , denoted by
, denoted by  , forms a group with respect to the operation of addition
, forms a group with respect to the operation of addition
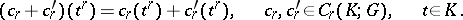 |
It is called the group of  -dimensional chains of
-dimensional chains of 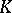 with coefficients in
with coefficients in 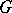 (or over
(or over 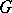 ). Under the hypothesis that
). Under the hypothesis that 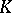 is a star-finite complex, one can introduce on
is a star-finite complex, one can introduce on 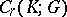 a boundary operator
a boundary operator 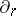 by means of the formula
by means of the formula
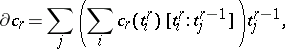 |
which defines a homomorphism
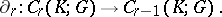 |
Because the equation 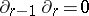 holds, one obtains a chain complex
holds, one obtains a chain complex 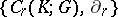 , whose homology group
, whose homology group 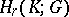 (i.e. the quotient group of
(i.e. the quotient group of  by the subgroup
by the subgroup 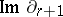 ) is called the
) is called the  -dimensional homology group of the complex
-dimensional homology group of the complex 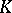 with coefficients in
with coefficients in 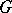 . (The group
. (The group 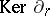 is often denoted by
is often denoted by 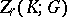 and is called the group of
and is called the group of  -dimensional cycles of the complex
-dimensional cycles of the complex  with coefficients in
with coefficients in 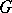 , while the group
, while the group 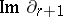 is denoted by
is denoted by 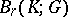 and is called the group of
and is called the group of  -dimensional boundaries of the complex
-dimensional boundaries of the complex 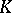 with coefficients in
with coefficients in 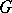 .)
.)
As well as homology groups, cohomology groups are also defined for a complex. For their definition, one starts again with a group of chains, called in this case the group of cochains, and denoted by 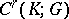 . The complex
. The complex 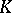 is here assumed to be closed-finite, while the coboundary operator
is here assumed to be closed-finite, while the coboundary operator 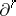 is defined by the formula
is defined by the formula
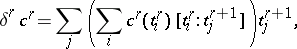 |
defining a homomorphism
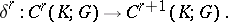 |
For this cochain complex 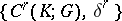 ,
, 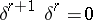 , the cohomology group
, the cohomology group 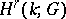 , i.e. the quotient group of
, i.e. the quotient group of 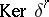 by the subgroup
by the subgroup 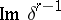 , is called the
, is called the  -dimensional cohomology group of the complex
-dimensional cohomology group of the complex 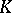 with coefficients in
with coefficients in 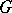 . (The group
. (The group  is usually denoted by
is usually denoted by 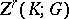 and is called the group of
and is called the group of  -dimensional cocycles of the complex
-dimensional cocycles of the complex 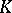 with coefficients in
with coefficients in 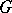 , while the group
, while the group 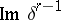 is denoted by
is denoted by 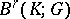 and is called the group of
and is called the group of  -dimensional coboundaries of the complex
-dimensional coboundaries of the complex 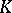 with coefficients in
with coefficients in 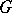 .)
.)
Star- (or closed-) finiteness of the complex is required in order that the summation in the definition of the boundary (or coboundary) operator be finite. In the case of a star-finite complex one can define the homology groups of arbitrary (infinite) cycles and the cohomology groups of finite cocycles. In the case of a closed-finite complex one can define the homology groups of infinite cocycles and the homology groups of finite cycles. In the case of a locally finite complex, one can define both finite and infinite homology and cohomology groups. If the complex is arbitrary, then its homology (respectively, cohomology) groups are defined as the direct (respectively, inverse) limit of the spectrum of the homology (respectively, cohomology) groups of all locally finite subcomplexes of the given complex, ordered by increasing size.
In the study of homology and cohomology groups of a complex one can consider the category of simplicial pairs of complexes 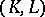 and simplicial mappings
and simplicial mappings 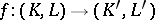 between them, and the group
between them, and the group 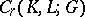 of
of  -dimensional finite chains of
-dimensional finite chains of 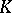 modulo
modulo 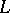 over
over 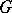 , this being the quotient group of the group
, this being the quotient group of the group 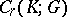 of
of  -dimensional chains of
-dimensional chains of 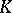 with coefficients in
with coefficients in 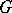 by the subgroup
by the subgroup 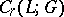 of
of  -dimensional chains of
-dimensional chains of  with coefficients in
with coefficients in 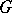 . The homology group
. The homology group 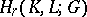 of the chain complex
of the chain complex 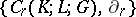 is called the
is called the  -dimensional relative homology group of the complex
-dimensional relative homology group of the complex 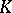 modulo
modulo 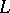 with coefficient group
with coefficient group 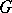 .
.
A simplicial mapping 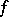 induces a homomorphism
induces a homomorphism 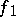 of the group
of the group 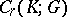 into the group
into the group 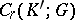 , according to the formula
, according to the formula
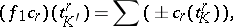 |
where 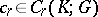 , and the sum extends over all simplices
, and the sum extends over all simplices  of
of  that are mapped onto the given simplex
that are mapped onto the given simplex 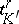 in
in 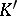 , where the sign
, where the sign 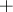 or
or  is chosen depending on whether or not the orientations of
is chosen depending on whether or not the orientations of 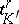 and
and 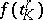 coincide. The homomorphism
coincide. The homomorphism 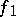 , extended to the quotient groups, induces a group homomorphism of
, extended to the quotient groups, induces a group homomorphism of 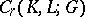 into
into 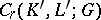 ; the latter homomorphism commutes with the boundary operator
; the latter homomorphism commutes with the boundary operator 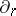 , so that one obtains a homomorphism of relative homology groups
, so that one obtains a homomorphism of relative homology groups
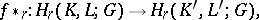 |
called the homomorphism induced by the simplicial mapping 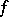 . The pair
. The pair 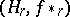 is a covariant functor from the category of simplicial pairs and simplicial mappings into the category of Abelian groups.
is a covariant functor from the category of simplicial pairs and simplicial mappings into the category of Abelian groups.
The inclusion mappings 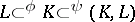 , where
, where 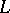 and
and 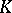 are the pairs
are the pairs  and
and  , induce the exact sequence
, induce the exact sequence
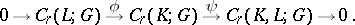 |
Let 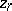 be an arbitrary cycle of the complex
be an arbitrary cycle of the complex 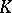 modulo
modulo 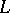 from any element
from any element  of the group
of the group 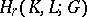 ; then there exists a chain
; then there exists a chain 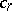 of
of 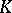 such that
such that 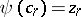 (
(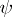 being an epimorphism), the chain
being an epimorphism), the chain 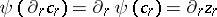 of the complex
of the complex 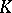 lies in
lies in 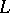 (that is, it vanishes on the simplices of
(that is, it vanishes on the simplices of 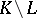 ) and belongs to
) and belongs to 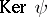 ; the chain that is equal to it — the inverse image
; the chain that is equal to it — the inverse image  under the monomorphism
under the monomorphism 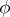 — is a cycle in the complex
— is a cycle in the complex  . By associating the homology class
. By associating the homology class 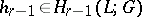 of the latter cycle with a given element
of the latter cycle with a given element 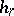 , one obtains a homomorphism
, one obtains a homomorphism
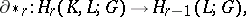 |
called the connecting homomorphism. It is compatible with the functor  , that is, the equation
, that is, the equation 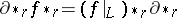 holds, where
holds, where 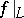 is the restriction of
is the restriction of 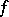 to
to 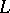 . The inclusion mappings
. The inclusion mappings 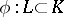 ,
, 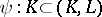 induce the exact sequence of groups
induce the exact sequence of groups
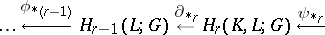 |
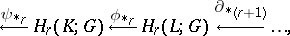 |
called the homology sequence of pairs 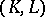 .
.
Two simplicial mappings 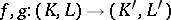 are said to be contiguous if for each simplex
are said to be contiguous if for each simplex  in
in 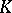 the simplices
the simplices 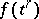 and
and 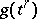 are faces of the same simplex in
are faces of the same simplex in 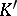 . In the category of simplicial pairs and their simplicial mappings, this relation plays the role of that of homotopy: For any contiguous simplicial mappings
. In the category of simplicial pairs and their simplicial mappings, this relation plays the role of that of homotopy: For any contiguous simplicial mappings 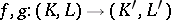 and any
and any  , the induced homomorphisms
, the induced homomorphisms 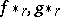 of the group
of the group 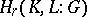 into the group
into the group 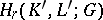 are the same.
are the same.
An imbedding 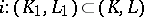 is called an excision mapping if
is called an excision mapping if 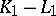 equals
equals 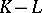 . The excision property is that every excision mapping
. The excision property is that every excision mapping  of simplicial pairs induces, for any
of simplicial pairs induces, for any  , an isomorphism
, an isomorphism 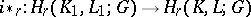 . The
. The  -dimensional homology group, with coefficient group
-dimensional homology group, with coefficient group 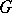 , of a complex
, of a complex 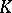 consisting of a single point is the zero group for all
consisting of a single point is the zero group for all  and is isomorphic to
and is isomorphic to  for
for  .
.
Thus, the triple 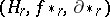 forms a homology theory in the sense of Steenrod–Eilenberg (see Steenrod–Eilenberg axioms).
forms a homology theory in the sense of Steenrod–Eilenberg (see Steenrod–Eilenberg axioms).
The cohomology theory is constructed in a similar fashion. The group  of
of  -dimensional infinite cochains of a complex
-dimensional infinite cochains of a complex 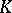 modulo the subcomplex
modulo the subcomplex 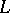 with coefficient group
with coefficient group 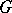 is the set of all
is the set of all  -dimensional cochains
-dimensional cochains 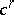 of
of 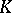 that vanish on the simplices
that vanish on the simplices 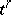 of
of 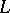 , while the
, while the  -dimensional relative cohomology group
-dimensional relative cohomology group 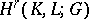 of the complex
of the complex 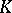 modulo
modulo 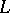 with coefficient group
with coefficient group 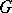 is the cohomology group of the cochain complex
is the cohomology group of the cochain complex 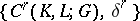 .
.
A simplicial mapping 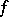 induces a homomorphism
induces a homomorphism 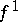 of the group
of the group  into the group
into the group 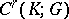 :
:
 |
The homomorphism 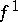 also induces a homomorphism of the group
also induces a homomorphism of the group  into the group
into the group  ; the latter homomorphism commutes with the coboundary operator
; the latter homomorphism commutes with the coboundary operator 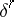 , and one obtains a homomorphism
, and one obtains a homomorphism 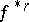 of the relative cohomology groups,
of the relative cohomology groups,
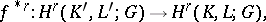 |
called the homomorphism induced by the simplicial mapping 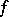 . The pair
. The pair 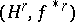 is a contravariant functor from the category of simplicial pairs and simplicial mappings into the category of Abelian groups.
is a contravariant functor from the category of simplicial pairs and simplicial mappings into the category of Abelian groups.
There is an exact sequence
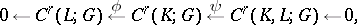 |
induced by the inclusions 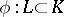 ,
, 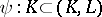 . Any cocycle
. Any cocycle 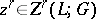 in the cohomology class
in the cohomology class 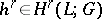 can, in an arbitrary way, be extended to a cochain
can, in an arbitrary way, be extended to a cochain  when
when 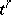 does not belong to the subcomplex
does not belong to the subcomplex 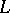 of
of 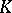 . The coboundary
. The coboundary 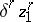 of the cochain thus obtained vanishes on
of the cochain thus obtained vanishes on 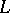 and belongs to the group
and belongs to the group 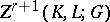 . The cohomology class
. The cohomology class 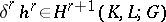 of this cocycle is put into correspondence with the selected class
of this cocycle is put into correspondence with the selected class 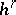 . This correspondence
. This correspondence 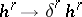 defines a homomorphism
defines a homomorphism
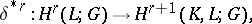 |
called connecting homomorphism. The homomorphism 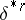 is compatible with the functor
is compatible with the functor 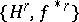 , in other words, the equation
, in other words, the equation 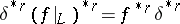 holds.
holds.
The sequence of groups and homomorphisms
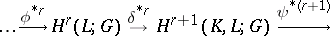 |
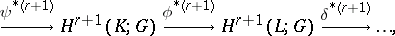 |
where 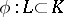 and
and 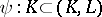 are the inclusion mappings, is an exact sequence and is called a cohomology sequence of the pair
are the inclusion mappings, is an exact sequence and is called a cohomology sequence of the pair 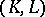 .
.
For any contiguous simplicial mappings 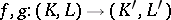 , and any
, and any  , the induced group homomorphisms
, the induced group homomorphisms 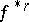 ,
,  of
of 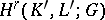 into
into 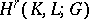 coincide; each excision mapping of simplicial pairs
coincide; each excision mapping of simplicial pairs 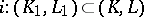 induces an isomorphism
induces an isomorphism 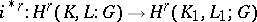 . For any complex
. For any complex 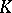 consisting of a single point,
consisting of a single point, 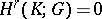 for all
for all 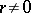 , and
, and 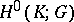 is isomorphic to
is isomorphic to 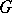 . Thus, the triple
. Thus, the triple 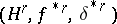 is a cohomology theory (in the sense of Steenrod–Eilenberg).
is a cohomology theory (in the sense of Steenrod–Eilenberg).
References
| [1] | P.S. Aleksandrov, "Combinatorial topology" , Graylock , Rochester (1956) (Translated from Russian) |
| [2] | P.S. Aleksandrov, "An introduction to homological dimension theory and general combinatorial topology" , Moscow (1975) (In Russian) |
| [3] | S. Lefschetz, "Algebraic topology" , Amer. Math. Soc. (1955) |
| [4] | P.J. Hilton, S. Wylie, "Homology theory. An introduction to algebraic topology" , Cambridge Univ. Press (1960) |
| [5] | L.S. Pontryagin, "Grundzüge der kombinatorischen Topologie" , Deutsch. Verlag Wissenschaft. (1956) (Translated from Russian) |
Comments
References
| [a1] | E.H. Spanier, "Algebraic topology" , McGraw-Hill (1966) |
| [a2] | R.M. Switzer, "Algebraic topology - homotopy and homology" , Springer (1975) |
Complex. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Complex&oldid=46427