Coefficient problem

for the class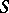

A problem for the class of functions

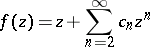which are regular and univalent in the disc 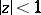. It consists of determining for every , , 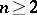the region of values 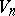for the system of coefficients 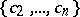of the functions of this class and, in particular, to find sharp bounds for 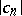, , 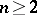in the class 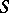(see Bieberbach conjecture). The coefficient problem for a class 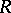of functions regular in 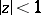consists in determining in 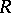, for every , , 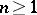the region of values of the first coefficients in the series expansions of the functions of in powers of and, in particular, in obtaining sharp bounds for these coefficients in the class 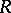. The coefficient problem has been solved for the Carathéodory class, for the class of univalent star-like functions, and for the class of functions regular and bounded in .

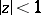It is known that 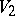is a disc: . Profound qualitative results with regard to the coefficient problem have been obtained for the class 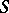(see [7]). The set 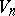is a bounded closed domain; the point 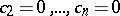is an interior point of 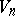; 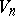is homeomorphic to a closed 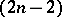-dimensional ball; the boundary of 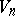is a union of finitely many parts 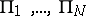; the coordinates of a point 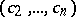on any one of these parts are functions of a finite number (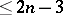) of parameters. To every boundary point of there corresponds a unique function of the class 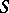. The boundary of 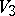is a union of two hyperplanes 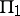and 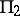of dimension 3 and their intersections: planes 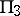and 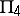and a curve 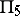. Parametric formulas have been derived for 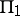and 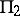in terms of elementary functions. The intersection of 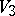with the plane 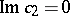is symmetric about the planes 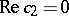and 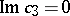. The intersection of 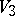with the plane 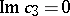is symmetric about the planes 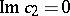and 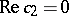. A function 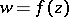corresponding to a point on 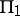maps 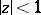onto the 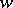-plane cut by an analytic curve going to infinity. 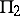A function corresponding to a point on maps 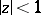onto the 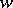-plane cut by three analytic arcs, issuing from a finite point and inclined to one another at angles 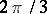; one of these arcs lies on a straight line 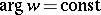and goes to infinity.

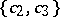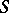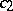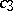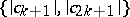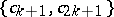Among the other special regions that have been investigated are the following: the region of values in the subclass of consisting of functions with real and ; the region of values and , if 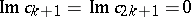, on the subclass of bounded functions in 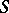representable as

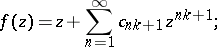the region of values 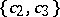on the subclass of bounded functions in 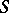; the region of values 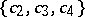on the subclass of functions in 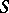with real 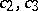and .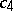

Sharp bounds for the coefficients, of the type 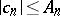, , 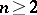have been obtained in the subclass of convex functions in 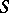with 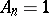(cf. Convex function (of a complex variable)), in the subclass of star-like functions in 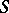with 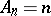, in the subclass of odd star-like functions in 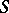with 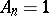, 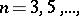in the class of univalent functions having real coefficients with 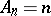, in the subclass of close-to-convex functions in 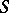with 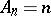, and in the class 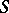itself with 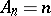(cf. Bieberbach conjecture, [8]). In the class of functions

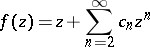which are regular and typically real in 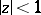one has the sharp bound 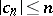, , 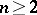and in the class of Bieberbach–Eilenberg functions 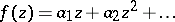one has the sharp bound , .

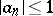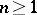Sharp bounds are known for the class 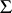of functions

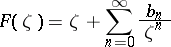which are meromorphic and univalent in 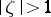; these are

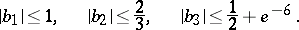For the subclass of star-like functions in 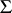, one has the sharp bound

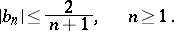Sharp bounds are also known for other subclasses of 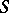and 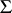(see [1]–[4]), and also for some classes of 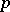-valent functions and in classes of functions which are 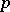-valent in the mean (see [5]).

References

[1]	G.M. Goluzin, "Geometric methods in the theory of functions of a complex variable" , Transl. Math. Monogr. , 26 , Amer. Math. Soc. (1969) (Translated from Russian)
[2]	I.E. Bazilevich, , Mathematics in the USSR during 40 years: 1917–1957 , 1 , Moscow (1959) pp. 444–472 (In Russian)
[3]	J.A. Jenkins, "Univalent functions and conformal mapping" , Springer (1958)
[4]	W.K. Hayman, "Coefficient problems for univalent functions and related function classes" J. London Math. Soc. , 40 : 3 (1965) pp. 385–406
[5]	A.W. Goodman, "Open problems on univalent and multivalent functions" Bull. Amer. Math. Soc. , 74 : 6 (1968) pp. 1035–1050
[6]	D. Phelps, "On a coefficient problem in univalent functions" Trans. Amer. Math. Soc. , 143 (1969) pp. 475–485
[7]	A.C. Schaeffer, D.C. Spencer, "Coefficient regions for schlicht functions" , Amer. Math. Soc. Coll. Publ. , 35 , Amer. Math. Soc. (1950)
[8]	L. de Branges, "A proof of the Bieberbach conjecture" Acta Math. , 154 : 1–2 (1985) pp. 137–152

Comments

For functions in the class 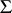, the estimates for 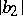and 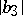mentioned above are due to M. Schiffer [a1] and P.R. Garabedian and Schiffer [a2], respectively. The sharp bound for star-like functions in 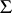is due to J. Clunie [a3] and C. Pommerenke [a4]. Standard references in English include [a5]–[a7].

References

[a1]	M. Schiffer, "Sur un problème d'extrémum de la répresentation conforme" Bull. Soc. Math. France , 66 (1938) pp. 48–55
[a2]	P.R. Garabedian, M. Schiffer, "A coefficient inequality for schlicht functions" Ann. of Math. , 61 (1955) pp. 116–136
[a3]	J. Clunie, "On meromorphic schlicht functions" J. London Math. Soc. , 34 (1959) pp. 215–216
[a4]	C. Pommerenke, "On meromorphic starlike functions" Pacific J. Math. , 13 (1963) pp. 221–235
[a5]	W.K. Hayman, "Multivalent functions" , Cambridge Univ. Press (1967)
[a6]	C. Pommerenke, "Univalent functions" , Vandenhoeck & Ruprecht (1975)
[a7]	P.L. Duren, "Univalent functions" , Springer (1983) pp. 258
[a8]	O. Tammi, "Extremum problems for bounded univalent functions II" , Lect. notes in math. , 913 , Springer (1982)