Clifford theory
(for group representations)
Let 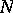 be a normal subgroup of a finite group
be a normal subgroup of a finite group  and let
and let  be the group algebra of
be the group algebra of 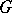 over a commutative ring
over a commutative ring 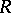 . Given an
. Given an 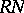 -module
-module 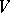 and
and 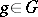 , let
, let 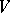 be the
be the  -module whose underlying
-module whose underlying 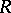 -module is
-module is 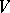 and on which
and on which  acts according to the rule
acts according to the rule  ,
,  , where
, where  denotes the module operation in
denotes the module operation in 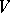 and
and 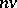 the operation in
the operation in 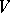 . By definition, the inertia group
. By definition, the inertia group 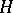 of
of 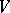 is
is 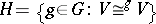 . It is clear that
. It is clear that 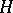 is a subgroup of
is a subgroup of 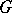 containing
containing 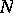 ; if
; if  , it is customary to say that
, it is customary to say that 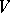 is
is 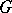 -invariant
-invariant
Important information concerning simple and indecomposable 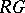 -modules can be obtained by applying (perhaps repeatedly) three basic operations:
-modules can be obtained by applying (perhaps repeatedly) three basic operations:
i) restriction to  ;
;
ii) extension from  ; and
; and
iii) induction from  . This is the content of the so-called Clifford theory, which was originally developed by A.H. Clifford (see [a1]) for the classical case where
. This is the content of the so-called Clifford theory, which was originally developed by A.H. Clifford (see [a1]) for the classical case where  is a field. General references for this area are [a2], [a3].
is a field. General references for this area are [a2], [a3].
The most important results are as follows.
Restriction to normal subgroups of representations.
Given a subgroup 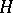 of
of 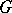 and an
and an  -module
-module 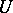 , let
, let  denote the restriction of
denote the restriction of 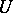 to
to  . If
. If 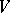 is an
is an  -module, then
-module, then  denotes the induced module. For any integer
denotes the induced module. For any integer  , let
, let 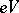 be the direct sum of
be the direct sum of  copies of a given module
copies of a given module 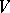 . A classical Clifford theorem, originally proved for the case where
. A classical Clifford theorem, originally proved for the case where 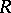 is a field, holds for an arbitrary commutative ring
is a field, holds for an arbitrary commutative ring  and asserts the following. Assume that
and asserts the following. Assume that 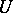 is a simple
is a simple  -module. Then there exists a simple submodule
-module. Then there exists a simple submodule 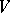 of
of 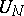 ; for any such
; for any such 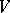 and the inertia group
and the inertia group 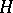 of
of 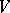 , the following properties hold.
, the following properties hold.
a)  , where
, where 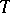 is a left transversal for
is a left transversal for 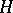 in
in 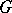 . Moreover, the modules
. Moreover, the modules 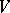 ,
,  , are pairwise non-isomorphic simple
, are pairwise non-isomorphic simple 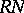 -modules.
-modules.
b) The sum 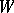 of all submodules of
of all submodules of  isomorphic to
isomorphic to 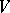 is a simple
is a simple  -module such that
-module such that  and
and  .
.
The above result holds in the more general case where  is a finite group. However, if
is a finite group. However, if  is infinite, then Clifford's theorem is no longer true (see [a3]).
is infinite, then Clifford's theorem is no longer true (see [a3]).
Induction from normal subgroups of representations.
The principal result concerning induction is the Green indecomposable theorem, described below. Assume that 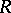 is a complete local ring and a principal ideal domain (cf. also Principal ideal ring). An integral domain
is a complete local ring and a principal ideal domain (cf. also Principal ideal ring). An integral domain 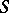 containing
containing 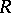 is called an extension, of
is called an extension, of 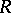 , written
, written  , if the following conditions hold:
, if the following conditions hold:
A) 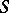 is a principal ideal domain and a local ring;
is a principal ideal domain and a local ring;
B) 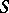 is
is 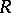 -free;
-free;
C)  for some integer
for some integer  . One says that
. One says that  is finite if
is finite if 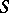 is a finitely generated
is a finitely generated 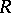 -module. An
-module. An 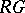 -module
-module 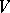 is said to be absolutely indecomposable if for every finite extension
is said to be absolutely indecomposable if for every finite extension  ,
, 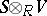 is an indecomposable
is an indecomposable 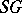 -module.
-module.
Assume that the field  is of prime characteristic
is of prime characteristic 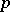 (cf. also Characteristic of a field) and that
(cf. also Characteristic of a field) and that  is a
is a 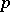 -group. If
-group. If  is a finitely generated absolutely indecomposable
is a finitely generated absolutely indecomposable 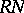 -module, then the induced module
-module, then the induced module 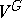 is absolutely indecomposable. Green's original statement pertained to the case where
is absolutely indecomposable. Green's original statement pertained to the case where 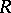 is a field. A proof in full generality is contained in [a3].
is a field. A proof in full generality is contained in [a3].
Extension from normal subgroups of representations.
The best result to date (1996) is Isaacs theorem, described below. Let  be a normal Hall subgroup of a finite group
be a normal Hall subgroup of a finite group 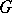 , let
, let 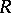 be an arbitrary commutative ring and let
be an arbitrary commutative ring and let 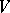 be a simple
be a simple 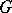 -invariant
-invariant  -module. Then
-module. Then 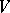 extends to an
extends to an 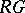 -module, i.e.
-module, i.e.  for some
for some 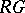 -module
-module  . Originally, R. Isaacs proved only the special case where
. Originally, R. Isaacs proved only the special case where 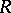 is a field. A proof in full generality can be found in [a3].
is a field. A proof in full generality can be found in [a3].
References
| [a1] | A.H. Clifford, "Representations induced in an invariant subgroup" Ann. of Math. (2) , 38 pp. 533–550 |
| [a2] | G. Karpilovsky, "Clifford theory for group representations" , North-Holland (1989) |
| [a3] | G. Karpilovsky, "Group representations" , 3 , North-Holland (1994) |
Clifford theory. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Clifford_theory&oldid=46360