Chebyshev constant

A numerical invariant of a compact set in the complex plane that is used in the theory of best approximation.

Let be the class of all polynomials

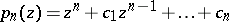of degree , and let

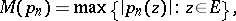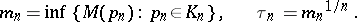There exists a polynomial for which ; it is called the Chebyshev polynomial for 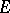. Moreover, the limit

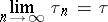exists, and is called the Chebyshev constant for .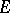

Restricting oneself to the class of all polynomials

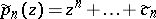all zeros of which lie in 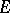, one obtains corresponding values 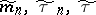and a polynomial for which (it is also called the Chebyshev polynomial).

It is known that 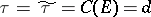, where 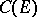is the capacity of the compact set , and 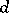is its transfinite diameter (cf., for example, [1]).

The concept of the Chebyshev constant generalizes to compact sets 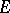in higher-dimensional Euclidean spaces starting from potential theory. For a poin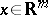t , let

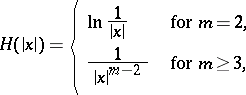be the fundamental solution of the Laplace equation, and for a set , let

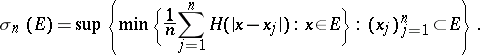Then for one obtains the relation

and for 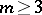one obtains (cf. [2]):

References

[1]	G.M. Goluzin, "Geometric theory of functions of a complex variable" , Transl. Math. Monogr. , 26 , Amer. Math. Soc. (1969) (Translated from Russian)
[2]	L. Carleson, "Selected problems on exceptional sets" , v. Nostrand (1967)

References

[a1]	M. Tsuji, "Potential theory in modern function theory" , Chelsea, reprint (1975)
[a2]	J.L. Walsh, "Interpolation and approximation by rational functions in the complex domain" , Amer. Math. Soc. (1956)