Characteristic function of a set
From Encyclopedia of Mathematics
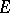 in a space
in a space 
The function  that is equal to 1 when
that is equal to 1 when  and equal to 0 when
and equal to 0 when  (where
(where 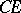 is the complement to
is the complement to 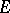 in
in 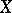 ). Every function
). Every function 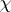 on
on 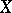 with values in
with values in 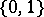 is the characteristic function of some set, namely, the set
is the characteristic function of some set, namely, the set 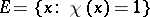 . Properties of characteristic functions are:
. Properties of characteristic functions are:
1) 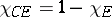 ,
, 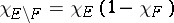 ;
;
2) if 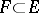 , then
, then  ;
;
3) if 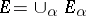 , then
, then 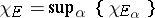 ;
;
4) if 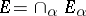 , then
, then 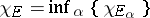 ;
;
5) if 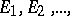 are pairwise disjoint, then
are pairwise disjoint, then 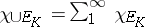 ;
;
6) if 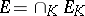 , then
, then 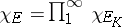 .
.
References
| [1] | P.R. Halmos, "Measure theory" , v. Nostrand (1950) |
Comments
The characteristic function of a set is also called the indicator function of that set. The symbols 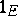 or
or 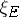 are often used instead of
are often used instead of 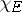 .
.
How to Cite This Entry:
Characteristic function of a set. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Characteristic_function_of_a_set&oldid=46320
Characteristic function of a set. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Characteristic_function_of_a_set&oldid=46320
This article was adapted from an original article by A.A. Konyushkov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article