Bredon cohomology
An ordinary equivariant cohomology for a finite group 
, defined in [a1], on the category 
-CW of 
-complexes (cf. Complex; CW-complex). The objects of 
-CW are the CW-complexes 
with a cellular action of 
, satisfying the condition that, for every subgroup 
of 
, the fixed point set 
is a subcomplex of 
. The morphisms are the cellular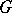 
-mappings. Let 
be the full subcategory of 
-CW whose objects are the 
-orbits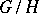 
, where 
is a subgroup of 
. For every contravariant functor 
from 
to the category 
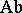of Abelian groups, there exists a Bredon cohomology theory 
which, after restriction to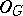 
, vanishes for 
and is equal to 
for 
.
Let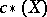 
be the chain complex of functors from 
to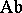 
such that, for every subgroup 
of 
, 
is the ordinary cellular chain complex of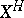 
. Then
 |
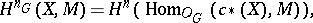where 
denotes the set of natural transformations of functors. The functors 
are projective objects in the category of coefficient systems and there is a spectral sequence
 |
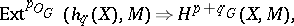where 
.
Let 
be a 
-space with base point 
(cf., e.g., Equivariant cohomology). Important examples of coefficient systems are the homotopy group functors 
defined by 
. The obstruction theory for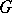 
-mappings 
is formulated in terms of the cohomology groups 
. For any coefficient system 
and natural number 
, there is a pointed Eilenberg–MacLane 
-complex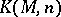 
such that 
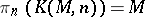and 
vanishes whenever 
. For every 
-complex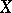 
, 
, where 
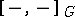denotes 
-homotopy classes of 
-mappings.
If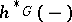 
is an equivariant cohomology theory defined on the category 
-CW, then there exists an Atiyah–Hirzebruch-type spectral sequence
 |
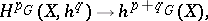where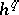 
is the restriction of 
to 
. Bredon cohomology for an arbitrary topological group is studied in [a4] and [a5]. Singular ordinary equivariant cohomology is defined in [a2] (the finite case) and in [a3]. If a coefficient system 
is a Mackey functor, then the Bredon cohomology 
can be extended to an ordinary 
-graded cohomology [a6].
References
| [a1] | G.E. Bredon, "Equivariant cohomology theories" , Lecture Notes in Mathematics , 34 , Springer (1967) |
| [a2] | T. Bröcker, "Singuläre Definition der äquivarianten Bredon Homologie" Manuscr. Math. , 5 (1971) pp. 91–102 |
| [a3] | S. Illman, "Equivariant singular homology and cohomology" , Memoirs , 156 , Amer. Math. Soc. (1975) |
| [a4] | T. Matumoto, "Equivariant cohomology theories on 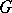 -CW-complexes" Osaka J. Math. , 10 (1973) pp. 51–68 |
| [a5] | S.J. Wilson, "Equivariant homology theories on 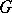 -complexes" Trans. Amer. Math. Soc. , 212 (1975) pp. 155–171 |
| [a6] | L.G. Lewis, J.P. May, J. McClure, "Ordinary RO(G)-graded cohomology" Bull. Amer. Math. Soc. , 4 (1981) pp. 208–212 |
Bredon cohomology. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bredon_cohomology&oldid=46160