Brauer-Severi variety
An algebraic variety over a field 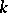 that, if considered over the algebraic closure
that, if considered over the algebraic closure 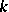 of
of 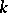 , becomes isomorphic to a projective space.
, becomes isomorphic to a projective space.
The arithmetic properties of such varieties were studied in 1932 by F. Severi; F. Châtelet subsequently discovered a connection between Brauer–Severi varieties and central simple algebras (cf. Central simple algebra) over 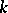 and the Brauer group.
and the Brauer group.
The simplest non-trivial example of a one-dimensional Brauer–Severi variety is the projective conic section 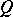 :
:
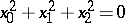 |
on the real projective plane  . Over the field of complex numbers
. Over the field of complex numbers 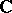 this variety is isomorphic to the projective line
this variety is isomorphic to the projective line 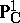 . The set of all one-dimensional Brauer–Severi varieties, considered up to isomorphism, is in a one-to-one correspondence with the set of projective non-degenerate conic sections (considered up to projective equivalence over
. The set of all one-dimensional Brauer–Severi varieties, considered up to isomorphism, is in a one-to-one correspondence with the set of projective non-degenerate conic sections (considered up to projective equivalence over 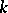 ), which is in turn in a one-to-one correspondence with the set of non-isomorphic generalized quaternion algebras over
), which is in turn in a one-to-one correspondence with the set of non-isomorphic generalized quaternion algebras over 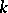 . In the above example the conical section
. In the above example the conical section 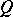 corresponds to the algebra of ordinary quaternions.
corresponds to the algebra of ordinary quaternions.
In the more-dimensional case, the set of classes of  -dimensional Brauer–Severi varieties (i.e. Brauer–Severi varieties distinguished up to
-dimensional Brauer–Severi varieties (i.e. Brauer–Severi varieties distinguished up to 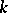 -isomorphism) may be identified with the Galois cohomology group
-isomorphism) may be identified with the Galois cohomology group 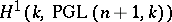 where
where 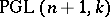 is the projective group of automorphisms of the projective space
is the projective group of automorphisms of the projective space 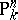 [3], [4]. This cohomology group describes the classes of
[3], [4]. This cohomology group describes the classes of 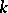 -isomorphic central simple
-isomorphic central simple 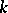 -algebras of rank
-algebras of rank 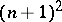 (i.e. forms of the matrix algebra
(i.e. forms of the matrix algebra 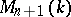 ). The connection between Brauer–Severi varieties and central simple algebras is more explicitly described as follows. To a
). The connection between Brauer–Severi varieties and central simple algebras is more explicitly described as follows. To a 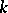 -algebra
-algebra 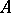 of rank
of rank  one associates the variety
one associates the variety 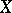 of its left ideals of rank
of its left ideals of rank  , which is defined as a closed subvariety of the Grassmann manifold of all
, which is defined as a closed subvariety of the Grassmann manifold of all 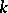 -linear subspaces of dimension
-linear subspaces of dimension  in
in 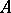 . In certain cases the variety
. In certain cases the variety 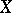 may be defined by norm equations — e.g. in the case of quaternion algebras. The connection between Brauer–Severi varieties and algebras is taken advantage of in the study of both [1], [4].
may be defined by norm equations — e.g. in the case of quaternion algebras. The connection between Brauer–Severi varieties and algebras is taken advantage of in the study of both [1], [4].
The most significant properties of Brauer–Severi varieties are the following. A Brauer–Severi variety is 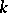 -isomorphic to a projective space
-isomorphic to a projective space 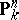 if and only if it has a point in the field
if and only if it has a point in the field 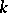 . All Brauer–Severi varieties have a point in some finite separable extension
. All Brauer–Severi varieties have a point in some finite separable extension 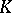 of
of 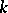 [1].
[1].
The Hasse principle applies to Brauer–Severi varieties defined over an algebraic number field.
The field of rational functions 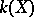 on a Brauer–Severi variety
on a Brauer–Severi variety 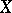 is the splitting field of the corresponding algebra
is the splitting field of the corresponding algebra 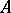 ; moreover, an arbitrary extension
; moreover, an arbitrary extension 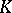 of
of 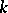 is the splitting field for
is the splitting field for 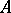 if and only if
if and only if 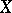 has a
has a 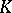 -point [4].
-point [4].
In the context of the generalization of the concepts of a central simple algebra and the Brauer group to include schemes, the Brauer–Severi varieties were generalized to the concept of Brauer–Severi schemes [2]. Let 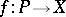 be a morphism of schemes. A scheme
be a morphism of schemes. A scheme 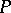 is called a Brauer–Severi scheme if it is locally isomorphic to a projective space
is called a Brauer–Severi scheme if it is locally isomorphic to a projective space 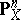 over
over 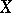 in the étale topology of
in the étale topology of 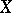 . A scheme
. A scheme 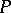 over a scheme
over a scheme 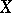 is a Brauer–Severi scheme if and only if
is a Brauer–Severi scheme if and only if 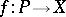 is a finitely-presented proper flat morphism and if all of its geometrical fibres are isomorphic to projective spaces [2].
is a finitely-presented proper flat morphism and if all of its geometrical fibres are isomorphic to projective spaces [2].
References
| [1] | F. Châtelet, "Variations sur un thème de H. Poincaré" Ann. Sci. École Norm. Sup. (3) , 61 (1944) pp. 249–300 |
| [2] | A. Grothendieck, "Le groupe de Brauer" A. Grothendieck (ed.) J. Giraud (ed.) et al. (ed.) , Dix exposés sur la cohomologie des schémas , North-Holland & Masson (1968) pp. 1–21 |
| [3] | J.-P. Serre, "Cohomologie Galoisienne" , Springer (1964) |
| [4] | P. Roguette, "On the Galois cohomology of the projective linear group and its applications to the construction of generic splitting fields of algebras" Math. Ann. , 150 (1963) pp. 411–439 |
Comments
Thus a Brauer–Severi variety of dimension  is a
is a 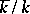 -form of
-form of 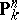 .
.
Brauer-Severi variety. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Brauer-Severi_variety&oldid=46157