Brafman polynomials

Polynomials given by

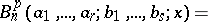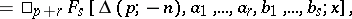where 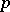is a positive integer, 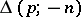abbreviates the set of 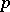parameters

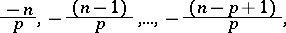and for non-negative integers and , denotes the generalized hypergeometric function (cf. also Hypergeometric function), defined by

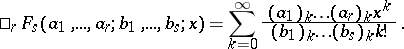The Brafman polynomials arise in the study of generating functions of orthogonal polynomials, [a1].

There are extensions. H.W. Gould and A.T. Hopper [a2] have considered special cases which sometimes reduce to the Hermite polynomials; see [a4] for a generalization. It is known [a3] that, in general, the Brafman polynomials cannot form an orthogonal set with respect to any weight function.

References

[a1]	F. Brafman, "Some generating functions for Laguerre and Hermite polynomials" Canadian J. Math. , 9 (1957) pp. 180–187
[a2]	H.W. Gould, A.T. Hopper, "Operational formulas connected with two generalizations of Hermite polynomials" Duke Math. J. , 29 (1962) pp. 51–63
[a3]	D. Mangeron, A.M. Krall, D.L. Fernandez, "Weight functions for some new classes of orthogonal polynomials" R. Acad. Cien. (Madrid) , 77 (1983) pp. 597–607
[a4]	R.M. Shreshtha, "On generalized Brafman polynomials" Comp. R. Acad. Bulgar. Sci. , 32 (1979) pp. 1183–1185