Boyd index
The lower and upper Boyd indices of a rearrangement-invariant function space 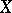 on
on 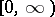 or
or 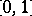 are defined by the respective formulas [a1]
are defined by the respective formulas [a1]
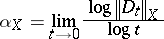 |
and
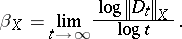 |
Here 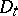 ,
, 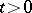 , is the dilation operator, i.e.
, is the dilation operator, i.e.
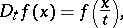 |
for a measurable function  on
on 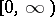 , while for an
, while for an  on
on 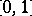 ,
,
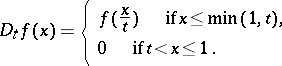 |
This operator is bounded in every rearrangement-invariant space 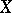 and the expression
and the expression 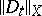 is its norm in
is its norm in  . The limits exist and
. The limits exist and 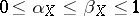 . Sometimes the indices are taken in the form
. Sometimes the indices are taken in the form 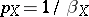 and
and 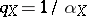 [a2].
[a2].
There are many applications of Boyd indices. The first one was made by D.W. Boyd [a1], who proved an interpolation theorem which gives, in terms of  and
and 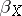 , the conditions for a linear operator of a weak type to be bounded in
, the conditions for a linear operator of a weak type to be bounded in  (cf. also Interpolation of operators).
(cf. also Interpolation of operators).
A necessary and sufficient condition for some classical operators to be bounded in  may be also obtained in terms of Boyd indices. For example, the Hardy–Littlewood operator
may be also obtained in terms of Boyd indices. For example, the Hardy–Littlewood operator
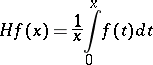 |
is bounded in  if and only if
if and only if 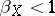 [a3].
[a3].
An important property of the class of rearrangement-invariant spaces with non-trivial Boyd indices was discovered in [a4]. Let 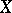 be a rearrangement-invariant space on
be a rearrangement-invariant space on 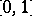 and denote by
and denote by 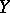 the space of all measurable functions on
the space of all measurable functions on 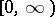 such that
such that 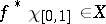 and
and  , where
, where 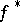 is the decreasing rearrangement (cf. also Marcinkiewicz space) of
is the decreasing rearrangement (cf. also Marcinkiewicz space) of 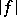 and
and  denotes the indicator of the set
denotes the indicator of the set 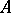 . Put
. Put
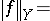 |
 |
If the strong inequalities  take place, then the spaces
take place, then the spaces  and
and 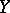 are isomorphic. In other words,
are isomorphic. In other words,  admits a representation as a rearrangement-invariant space on
admits a representation as a rearrangement-invariant space on 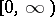 .
.
References
| [a1] | D.W. Boyd, "Indices of function spaces and their relationship to interpolation" Canadian J. Math. , 21 (1969) pp. 1245–1254 |
| [a2] | J. Lindenstrauss, L. Tzafriri, "Classical Banach spaces" , II. Function spaces , Springer (1979) |
| [a3] | S.G. Krein, E.M. Semenov, Yu.I. Petunin, "Interpolation of linear operators" , Transl. Math. Monograph , 54 , Amer. Math. Soc. (1982) (In Russian) |
| [a4] | W.B. Johnson, B. Maurey, G. Schechtman, L. Tzafriri, "Symmetric structures in Banach spaces" , Memoirs , 217 , Amer. Math. Soc. (1979) pp. 1–298 |
Boyd index. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Boyd_index&oldid=46142