Boundary correspondence, principle of
A principle formulated in the following way. One says that the principle of boundary correspondence holds for a mapping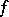 
if the facts that 
is a continuous mapping of the closure 
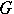of a domain 
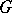onto the closure 
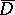of a domain 
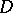and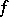 
is a homeomorphism of 
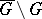onto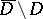 
imply that 
is a topological mapping of 
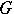onto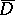 
. Thus, the principle of boundary correspondence is in some sense converse to the boundary-correspondence principle (cf. Boundary correspondence (under conformal mapping)).
If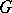 
and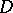 
are plane domains with Euclidean boundaries homeomorphic to a circle and 
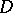is bounded, then the principle of boundary correspondence holds for analytic functions 
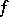on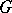 
, i.e. 
is a conformal mapping of 
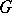onto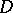 
. In addition to that given above, various other forms of the principle of boundary correspondence are commonly used for conformal mappings (see [1]). The principle of boundary correspondence has been verified for orientable mappings in Euclidean space (see [2]).
References
| [1] | M.A. Lavrent'ev, B.V. Shabat, "Methoden der komplexen Funktionentheorie" , Deutsch. Verlag Wissenschaft. (1967) (Translated from Russian) |
| [2] | L.D. Kudryavtsev, "On differentiable mappings" Dokl. Akad. Nauk SSSR , 95 : 5 (1954) pp. 921–923 (In Russian) |
| [3] | S.I. Pinchuk, "Holomorphic equivalence of certain classes of domains in 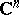 " Math. USSR-Sb. , 111 (153) : 1 (180) pp. 67–94; 159 Mat. Sb. , 111 (153) : 1 (1980) pp. 67–94; 159 |
Boundary correspondence, principle of. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Boundary_correspondence,_principle_of&oldid=46128