Best linear unbiased estimator
BLUE
Let
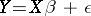 | (a1) |
be a linear regression model, where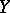 
is a random column vector of 
"measurements" , 
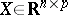is a known non-random "plan" matrix, 
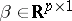is an unknown vector of the parameters, and 
is a random "error" , or "noise" , vector with mean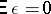 
and a possibly unknown non-singular covariance matrix 
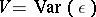. A model with linear restrictions on 
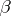can be obviously reduced to (a1). Without loss of generality, 
.
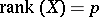Let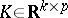 
; a linear unbiased estimator (LUE) of 
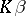is a statistical estimator of the form 
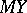for some non-random matrix 
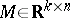such that 
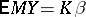for all 
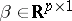, i.e., 
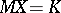. A linear unbiased estimator 
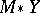of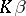 
is called a best linear unbiased estimator (BLUE) of 
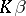if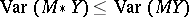 
for all linear unbiased estimators 
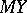of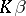 
, i.e., if 
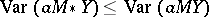for all linear unbiased estimators 
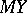of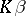 
and all 
.
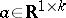Since it is assumed that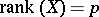 
, there exists a unique best linear unbiased estimator of 
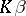for any 
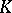. It is then given by the formula 
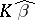, where 
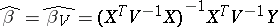, which coincides by the Gauss–Markov theorem (cf. Least squares, method of) with the least square estimator of 
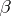, defined as 
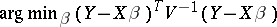; as usual, 
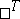stands for transposition.
Because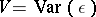 
is normally not known, Yu.A. Rozanov [a2] has suggested to use a "pseudo-best" estimator 
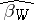in place of 
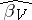, with an appropriately chosen 
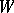. This idea has been further developed by A.M. Samarov [a3] and I.F. Pinelis [a4]. In particular, Pinelis has obtained duality theorems for the minimax risk and equations for the minimax solutions 
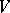assumed to belong to an arbitrary known convex set 
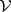of positive-definite 
-matrices with respect to the general quadratic risk function of the form
 |
 |
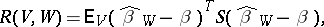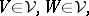where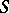 
is any non-negative-definite 
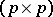-matrix and 
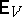stands for the expectation assuming 
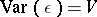. Asymptotic versions of these results have also been given by Pinelis for the case when the "noise" is a second-order stationary stochastic process with an unknown spectral density belonging to an arbitrary, but known, convex class of spectral densities and by Samarov in the case of contamination classes.
References
| [a1] | C.R. Rao, "Linear statistical inference and its applications" , Wiley (1965) |
| [a2] | Yu.A. Rozanov, "On a new class of estimates" , Multivariate Analysis , 2 , Acad. Press (1969) pp. 437–441 |
| [a3] | A.M. Samarov, "Robust spectral regression" Ann. Math. Stat. , 15 (1987) pp. 99–111 |
| [a4] | I.F. Pinelis, "On the minimax estimation of regression" Th. Probab. Appl. , 35 (1990) pp. 500–512 |
Best linear unbiased estimator. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Best_linear_unbiased_estimator&oldid=46043