Bessel polynomials
From Encyclopedia of Mathematics
Related to Bessel functions, [a2], the Bessel polynomials  satisfy
satisfy
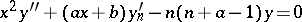 |
and are given by
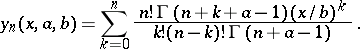 |
The ordinary Bessel polynomials are those found with  , [a2].
, [a2].
The moments associated with the Bessel polynomials satisfy
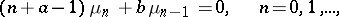 |
and are given by  .
.
The weight equation is
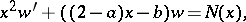 |
where  is any function with
is any function with  moments. This equation has been solved when
moments. This equation has been solved when
 |
where
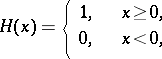 |
when  (no restriction),
(no restriction),  and
and  , [a3]. The weight for the ordinary Bessel polynomials was found by S.S. Kim, K.H. Kwon and S.S. Han, [a1], after over 40 years of search.
, [a3]. The weight for the ordinary Bessel polynomials was found by S.S. Kim, K.H. Kwon and S.S. Han, [a1], after over 40 years of search.
Using the three-term recurrence relation
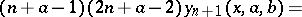 |
 |
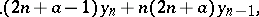 |
the norm square  is easily calculated and equals
is easily calculated and equals  , [a2], where
, [a2], where 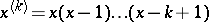 . Clearly,
. Clearly, 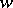 generates a Krein space on
generates a Krein space on 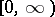 .
.
References
| [a1] | S.S. Kim, K.H. Kwon, S.S. Han, "Orthogonalizing weights of Tchebychev sets of polynomials" Bull. London Math. Soc. , 24 (1992) pp. 361–367 |
| [a2] | H.L. Krall, O. Frink, "A new class of orthogonal polynomials: The Bessel polynomials" Trans. Amer. Math. Soc. , 63 (1949) pp. 100–115 |
| [a3] | P. Maroni, "An integral representation for the Bessel form" J. Comp. Appl. Math. , 57 (1995) pp. 251–260 |
How to Cite This Entry:
Bessel polynomials. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bessel_polynomials&oldid=46035
Bessel polynomials. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bessel_polynomials&oldid=46035
This article was adapted from an original article by A.M. Krall (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article