A formula which is defined as half the sum of the Gauss formula (cf. Gauss interpolation formula) for forward interpolation on the nodes
at the point 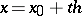 :
:
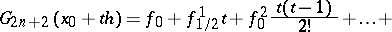 | (1) |
and the Gauss formula of the same order for backward interpolation with respect to the node 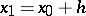 , i.e. with respect to the population of nodes
, i.e. with respect to the population of nodes
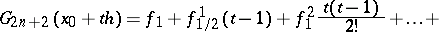 | (2) |
Putting
Bessel's interpolation formula assumes the form ([1], [2]):
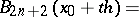 | (3) |
Bessel's interpolation formula has certain advantages over Gauss' formulas (1), (2); in particular, if the interpolation is at the middle of the segment, i.e. at 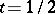 , all coefficients at the differences of odd orders vanish. If the last term on the right-hand side of (3) is omitted, the polynomial
, all coefficients at the differences of odd orders vanish. If the last term on the right-hand side of (3) is omitted, the polynomial 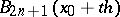 , which is not a proper interpolation polynomial (it coincides with
, which is not a proper interpolation polynomial (it coincides with 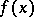 only in the
only in the 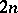 nodes
nodes 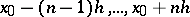 ), represents a better estimate of the residual term (cf. Interpolation formula) than the interpolation polynomial of the same degree. Thus, for instance, if
), represents a better estimate of the residual term (cf. Interpolation formula) than the interpolation polynomial of the same degree. Thus, for instance, if 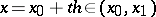 , the estimate of the last term using the polynomial which is most frequently employed
, the estimate of the last term using the polynomial which is most frequently employed
written with respect to the nodes 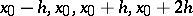 , is almost 8 times better than that of the interpolation polynomial written with respect to the nodes
, is almost 8 times better than that of the interpolation polynomial written with respect to the nodes 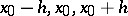 or
or 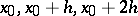 ([2]).
([2]).
References
| [1] | I.S. Berezin, N.P. Zhidkov, "Computing methods" , 1 , Pergamon (1973) (Translated from Russian) |
| [2] | N.S. Bakhvalov, "Numerical methods: analysis, algebra, ordinary differential equations" , MIR (1977) (Translated from Russian) |
References
| [a1] | M. Abramowitz, I.A. Stegun, "Handbook of mathematical functions" , Dover, reprint (1970) |
| [a2] | F.B. Hildebrand, "Introduction to numerical analysis" , Addison-Wesley (1956) |
How to Cite This Entry:
Bessel interpolation formula. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bessel_interpolation_formula&oldid=46034
This article was adapted from an original article by M.K. Samarin (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098.
See original article
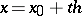 :
:
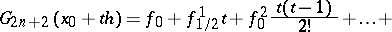
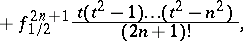
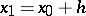 , i.e. with respect to the population of nodes
, i.e. with respect to the population of nodes
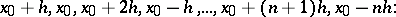
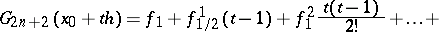
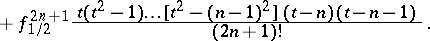
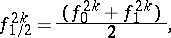
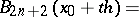
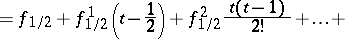
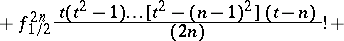
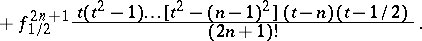
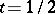 , all coefficients at the differences of odd orders vanish. If the last term on the right-hand side of (3) is omitted, the polynomial
, all coefficients at the differences of odd orders vanish. If the last term on the right-hand side of (3) is omitted, the polynomial 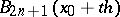 , which is not a proper interpolation polynomial (it coincides with
, which is not a proper interpolation polynomial (it coincides with 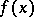 only in the
only in the 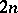 nodes
nodes 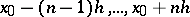 ), represents a better estimate of the residual term (cf. Interpolation formula) than the interpolation polynomial of the same degree. Thus, for instance, if
), represents a better estimate of the residual term (cf. Interpolation formula) than the interpolation polynomial of the same degree. Thus, for instance, if 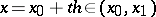 , the estimate of the last term using the polynomial which is most frequently employed
, the estimate of the last term using the polynomial which is most frequently employed
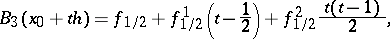
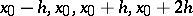 , is almost 8 times better than that of the interpolation polynomial written with respect to the nodes
, is almost 8 times better than that of the interpolation polynomial written with respect to the nodes 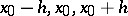 or
or 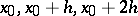 ([2]).
([2]).