Baer multiplication

A binary operation on the set of classes of extensions of modules, proposed by R. Baer [1]. Let 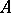and 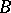be arbitrary modules. An extension of 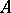with kernel 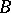is an exact sequence:

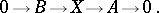(1)

The extension (1) is called equivalent to the extension

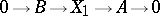if there exists a homomorphism 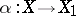forming part of the commutative diagram

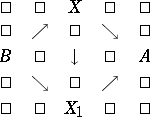The set of equivalence classes of extensions is denoted by 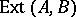. The Baer multiplication on 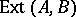is induced by the operation of products of extensions defined as follows. Let

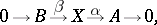(2)

(3)

be two extensions. In the direct sum the submodules

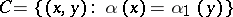and

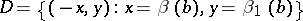are selected. Clearly, 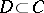, so that one can define the quotient module 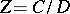. The Baer product of the extensions (2) and (3) is the extension

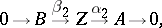where

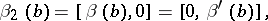and

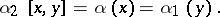References

[1]	R. Baer, "Erweiterung von Gruppen und ihren Isomorphismen" Math. Z. , 38 (1934) pp. 374–416
[2]	H. Cartan, S. Eilenberg, "Homological algebra" , Princeton Univ. Press (1956)