Genetic algebra

Let be a non-associative, commutative algebra of dimension over a field .

Let the field be an algebraic extension of , and let be the extension of over (cf. also Extension of a field). Let admit a basis 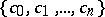, , 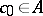with multiplication constants 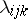, defined by

which have the following properties:

,

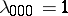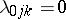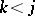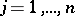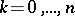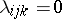for , ; ,

for , ; .

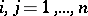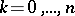Then 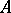is called a genetic algebra and 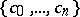is called a canonical basis of . The multiplication constants 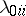, , 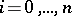are invariants of a genetic algebra; they are called the train roots of .

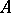An algebra 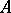is called a baric algebra if there exists a non-trivial algebra homomorphism 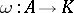; 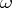is called a weight homomorphism or simply a weight. Every genetic algebra is baric with 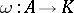defined by 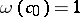, , 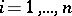; and is an -dimensional ideal of .

Let 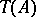be the transformation algebra of the algebra , i.e. the algebra generated by the (say) left transformations 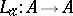, , , 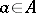and the identity.

A non-associative, commutative algebra is a genetic algebra if and only if for every 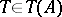, , 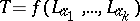the coefficients of the characteristic polynomial are functions of only.

Historically, genetic algebras were first defined by this property (R.D. Schafer [a5]). H. Gonshor [a3] proved the equivalence with the first definition above. P. Holgate [a4] proved that in a baric algebra 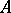the weight 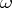is uniquely determined if 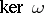is a nil ideal.

Algebras in genetics originate from the work of I.M.H. Etherington [a2], who put the Mendelian laws into an algebraic form. Consider an infinitely large, random mating population of diploid (or 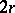-ploid) individuals which differ genetically at one or several loci. Let be the genetically different gametes. The state of the population can be described by the vector of frequencies of gametes,

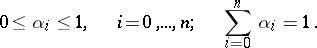By random union of gametes 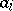and 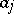, zygotes 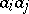are formed, 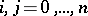. In the absence of selection all zygotes have the same fertility. Let be the relative frequency of gametes , , 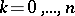produced by a zygote , ,

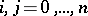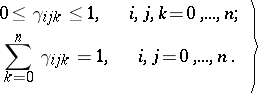(a1)

Let the segregation rates 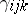be symmetric, i.e.

(a2)

Consider the elements as abstract elements which are free over the field 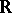. In the vector space 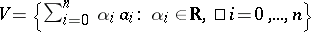a multiplication is defined by

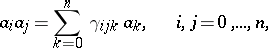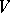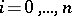and its bilinear extension onto . Thereby becomes a commutative algebra , the gametic algebra. Actual populations correspond to elements with , , and 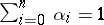. Random union of populations corresponds to multiplication of the corresponding elements in the algebra . Under rather general assumptions (including mutation, crossing over, polyploidy) gametic algebras are genetic algebras. Examples can be found in [a2] or [a7].

The zygotic algebra 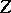is obtained from the gametic algebra 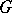by duplication, i.e. as the symmetric tensor product of with itself:

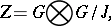(a3)

where

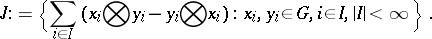The zygotic algebra describes the evolution of a population of diploid (-ploid) individuals under random mating.

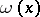A baric algebra with weight is called a train algebra if the coefficients of the rank polynomial of all principal powers of depend only on , i.e. if this polynomial has the form

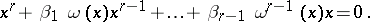(a4)

A baric algebra 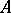with weight 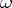is called a special train algebra if is nilpotent and the principal powers 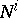, , are ideals of , cf. [a2]. Etherington [a2] proved that every special train algebra is a train algebra. Schafer [a5] showed that every special train algebra is a genetic algebra and that every genetic algebra is a train algebra. Further characterizations of these algebras can be found in [a7], Chapts. 3, 4.

Let be a baric algebra with weight . If all elements of 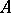satisfy the identity

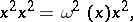then 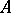is called a Bernstein algebra. Every Bernstein algebra possesses an idempotent . The decomposition with respect to this idempotent reads

where

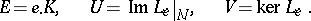The integers 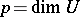and 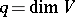are invariants of 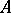, the pair 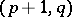is called the type of the Bernstein algebra 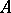, cf. [a7], Chapt. 9. In [a6] necessary and sufficient conditions have been given for a Bernstein algebra to be a Jordan algebra.

Bernstein algebras were introduced by S. Bernstein [a1] as a generalization of the Hardy–Weinberg law, which states that a randomly mating population is in equilibrium after one generation.

References

[a1]	S. Bernstein, "Principe de stationarité et généralisation de la loi de Mendel" C.R. Acad. Sci. Paris , 177 (1923) pp. 581–584
[a2]	I.M.H. Etherington, "Genetic algebras" Proc. R. Soc. Edinburgh , 59 (1939) pp. 242–258
[a3]	H. Gonshor, "Contributions to genetic algebras" Proc. Edinburgh Math. Soc. (2) , 17 (1971) pp. 289–298
[a4]	P. Holgate, "Characterizations of genetic algebras" J. London Math. Soc. (2) , 6 (1972) pp. 169–174
[a5]	R.D. Schafer, "Structure of genetic algebras" Amer. J. Math. , 71 (1949) pp. 121–135
[a6]	S. Walcher, "Bernstein algebras which are Jordan algebras" Arch. Math. , 50 (1988) pp. 218–222
[a7]	A. Wörz-Busekros, "Algebras in genetics" , Lect. notes in biomath. , 36 , Springer (1980)