Asymptotic optimality

of estimating functions

Efficient estimation (cf. Efficient estimator) of parameters in stochastic models is most conveniently approached via properties of estimating functions, namely functions of the data and the parameter of interest, rather than estimators derived therefrom. For a detailed explanation see [a1], Chapt. 1.

Let be a sample in discrete or continuous time from a stochastic system taking values in an -dimensional Euclidean space. The distribution of depends on a parameter of interest taking values in an open subset of a -dimensional Euclidean space. The possible probability measures (cf. Probability measure) for are , a union of families of models.

Consider the class of zero-mean square-integrable estimating functions , which are vectors of dimension and for which the matrices used below are non-singular.

Optimality in both the fixed sample and the asymptotic sense is considered. The former involves choice of an estimating function 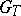to maximize, in the partial order of non-negative definite matrices, the information criterion

which is a natural generalization of the Fisher amount of information. Here is the -matrix of derivatives of the elements of with respect to those of 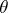and prime denotes transposition. If is a prespecified family of estimating functions, it is said that is fixed sample optimal in if 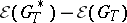is non-negative definite for all , 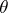and . Then, is the element of whose dispersion distance from the maximum information estimating function in (often the likelihood score) is least.

A focus on asymptotic properties can be made by confining attention to the subset 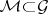of estimating functions which are martingales (cf. Martingale). Here one considers 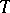ranging over the positive real numbers and for one writes 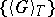for the quadratic characteristic, the predictable increasing process for which is a martingale. Also, write for the predictable process for which is a martingale. 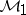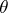Then, is asymptotically optimal in if is almost surely non-negative definite for all , , , and 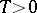, where

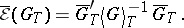Under suitable regularity conditions, asymptotically optimal estimating functions produce estimators for which are consistent (cf. Consistent estimator), asymptotically unbiased (cf. Unbiased estimator) and asymptotically normally distributed (cf. Normal distribution) with minimum size asymptotic confidence zones (cf. Confidence estimation). For further details see [a2], [a3].

References

[a1]	D.L. McLeish, C.G. Small, "The theory and applications of statistical inference functions" , Lecture Notes in Statistics , Springer (1988)
[a2]	V.P. Godambe, C.C. Heyde, "Quasi-likelihood and optimal estimation" Internat. Statist. Rev. , 55 (1987) pp. 231–244.
[a3]	C.C. Heyde, "Quasi-likelihood and its application. A general approach to optimal parameter estimation" , Springer (1997)