Asymptotically-unbiased estimator
A concept indicating that the estimator is unbiased in the limit (cf. Unbiased estimator). Let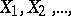 
be a sequence of random variables on a probability space 
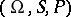, where 
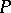is one of the probability measures in a family 
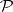. Let a function 
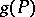be given on the family 
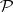, and let there be a sequence of 
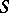-measurable functions 
, 
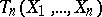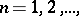the mathematical expectations of which, 
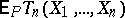, are given. Then, if, as 
,
 |
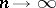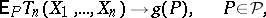one says that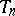 
is a function which is asymptotically unbiased for the function 
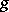. If one calls 
"observations" and 
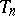"estimators" , one obtains the definition of an asymptotically-unbiased estimator. In the simplest case of unlimited repeated sampling from a population, the distribution of which depends on a one-dimensional parameter 
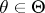, an asymptotically-unbiased estimat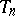or 
for 
, constructed with respect to the sample size 
, satisfies the condition
 |
for any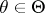 
, as 
.
Asymptotically-unbiased estimator. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Asymptotically-unbiased_estimator&oldid=45236