Absolutely summing operator
A linear operator  acting from a Banach space
acting from a Banach space  into a Banach space
into a Banach space  is called absolutely
is called absolutely  -summing (
-summing ( ) if there is a constant
) if there is a constant  such that
such that
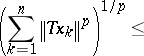 |
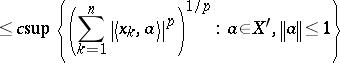 |
whenever 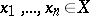 and
and  . Here,
. Here, 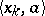 denotes the value of the linear functional
denotes the value of the linear functional 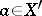 (the Banach dual of
(the Banach dual of 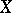 , cf. Adjoint space) at the element
, cf. Adjoint space) at the element 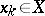 . The set of such operators, denoted by
. The set of such operators, denoted by 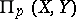 , becomes a Banach space under the norm
, becomes a Banach space under the norm  , and
, and 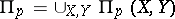 is a Banach operator ideal. If
is a Banach operator ideal. If  , then
, then 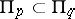 .
.
The prototype of an absolutely  -summing operator is the canonical mapping
-summing operator is the canonical mapping 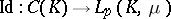 , where
, where 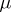 is a Borel measure on a compact Hausdorff space
is a Borel measure on a compact Hausdorff space 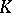 . In this case,
. In this case, 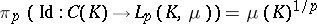 .
.
The famous Grothendieck theorem says that all operators from  into any Hilbert space are absolutely
into any Hilbert space are absolutely 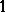 -summing.
-summing.
Absolutely 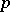 -summing operators are weakly compact but may fail to be compact (cf. also Compact operator). For a Hilbert space
-summing operators are weakly compact but may fail to be compact (cf. also Compact operator). For a Hilbert space 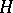 it turns out that
it turns out that 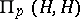 is just the set of Hilbert–Schmidt operators (cf. Hilbert–Schmidt operator). Nuclear operators (cf. Nuclear operator) are absolutely
is just the set of Hilbert–Schmidt operators (cf. Hilbert–Schmidt operator). Nuclear operators (cf. Nuclear operator) are absolutely 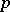 -summing. Conversely, the product of
-summing. Conversely, the product of 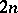 absolutely
absolutely 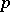 -summing operators is nuclear, hence compact, if
-summing operators is nuclear, hence compact, if 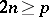 . This implies that the identity mapping of a Banach space
. This implies that the identity mapping of a Banach space 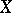 is absolutely
is absolutely 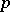 -summing if and only if
-summing if and only if 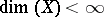 (the Dvoretzky–Rogers theorem).
(the Dvoretzky–Rogers theorem).
References
| [a1] | J. Diestel, H. Jarchow, A. Tonge, "Absolutely summing operators" , Cambridge Univ. Press (1995) |
| [a2] | G.J.O. Jameson, "Summing and nuclear norms in Banach space theory" , Cambridge Univ. Press (1987) |
| [a3] | A. Pietsch, "Operator ideals" , North-Holland (1980) |
Absolutely summing operator. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Absolutely_summing_operator&oldid=45003