Fourier transform
One of the integral transforms (cf. Integral transform). It is a linear operator $F$ acting on a space whose elements are functions $f$ of $n$ real variables. The smallest domain of definition of $F$ is the set $D=C_0^\infty$ of all infinitely-differentiable functions $\phi$ of compact support. For such functions
\begin{equation} (F\phi)(x) = \frac{1}{(2\pi)^{\frac{n}{2}}} \cdot \int_{\mathbf R^n} \phi(\xi) e^{-i x \xi} \, \mathrm d\xi. \end{equation}
In a certain sense the most natural domain of definition of $F$ is the set $S$ of all infinitely-differentiable functions $\phi$ that, together with their derivatives, vanish at infinity faster than any power of $\frac{1}{|x|}$. Formula (1) still holds for $\phi\in S$, and $(F \phi)(x) \equiv \psi(x)\in S$. Moreover, $F$ is an isomorphism of $S$ onto itself, the inverse mapping $F^{-1}$ (the inverse Fourier transform) is the inverse of the Fourier transform and is given by the formula:
\begin{equation} \phi(x) = (F^{-1} \psi)(x) = \frac{1}{(2\pi)^{\frac{n}{2}}} \cdot \int_{\mathbf R^n} \psi(\xi) e^{i x \xi} \, \mathrm d\xi. \end{equation}
Formula (1) also acts on the space $L_{1}\left(\mathbf{R}^{n}\right)$ of integrable functions. In order to enlarge the domain of definition of the operator $F$ generalization of (1) is necessary. In classical analysis such a generalization has been constructed for locally integrable functions with some restriction on their behaviour as $|x|\to\infty$ (see Fourier integral). In the theory of generalized functions the definition of the operator $F$ is free of many requirements of classical analysis.
The basic problems connected with the study of the Fourier transform $F$ are: the investigation of the domain of definition 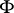 and the range of values
and the range of values 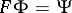 of
of 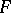 ; as well as studying properties of the mapping
; as well as studying properties of the mapping 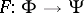 (in particular, conditions for the existence of the inverse operator
(in particular, conditions for the existence of the inverse operator 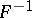 and its expression). The inversion formula for the Fourier transform is very simple:
and its expression). The inversion formula for the Fourier transform is very simple:
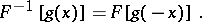 |
Under the action of the Fourier transform linear operators on the original space, which are invariant with respect to a shift, become (under certain conditions) multiplication operators in the image space. In particular, the convolution of two functions 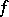 and
and 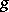 goes over into the product of the functions
goes over into the product of the functions  and
and 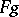 :
:
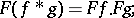 |
and differentiation induces multiplication by the independent variable:
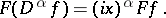 |
In the spaces 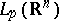 ,
, 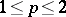 , the operator
, the operator 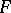 is defined by the formula (1) on the set
is defined by the formula (1) on the set 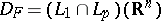 and is a bounded operator from
and is a bounded operator from 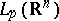 into
into 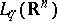 ,
, 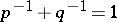 :
:
\begin{equation} \left\{\frac{1}{(2 \pi)^{n / 2}} \int_{\mathbf{R}^{n}}|(F f)(x)|^{q} d x\right\}^{1 / q} \leq\left\{\frac{1}{(2 \pi)^{n / 2}} \int_{\mathbf{R}^{n}}|f(x)|^{p} d x\right\}^{1 / p} \end{equation}
(the Hausdorff–Young inequality).  admits a continuous extension onto the whole space
admits a continuous extension onto the whole space 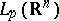 which (for
which (for 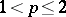 ) is given by
) is given by
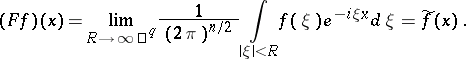 | (3) |
Convergence is understood to be in the norm of 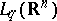 . If
. If 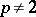 , the image of
, the image of 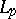 under the action of
under the action of 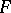 does not coincide with
does not coincide with 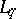 , that is, the imbedding
, that is, the imbedding 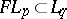 is strict when
is strict when 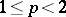 (for the case
(for the case 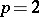 see Plancherel theorem). The inverse operator
see Plancherel theorem). The inverse operator 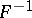 is defined on
is defined on 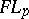 by
by
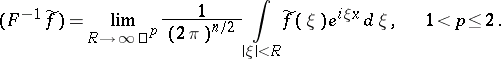 |
The problem of extending the Fourier transform to a larger class of functions arises constantly in analysis and its applications. See, for example, Fourier transform of a generalized function.
References
| [1] | E.C. Titchmarsh, "Introduction to the theory of Fourier integrals" , Oxford Univ. Press (1948) |
| [2] | A. Zygmund, "Trigonometric series" , 2 , Cambridge Univ. Press (1988) |
| [3] | E.M. Stein, G. Weiss, "Fourier analysis on Euclidean spaces" , Princeton Univ. Press (1971) |
Comments
Instead of "generalized function" the term "distributiondistribution" is often used.
If 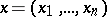 and
and 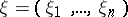 then
then  denotes the scalar product
denotes the scalar product 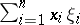 .
.
If in (1) the "normalizing factor" 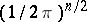 is replaced by some constant
is replaced by some constant  , then in (2) it must be replaced by
, then in (2) it must be replaced by 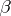 with
with 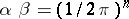 .
.
At least two other conventions for the "normalization factor" are in common use:
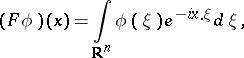 | (a1) |
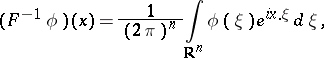 |
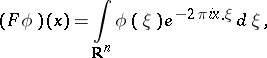 | (a2) |
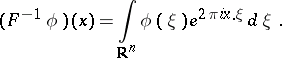 |
The convention of the article leads to the Fourier transform as a unitary operator from  into itself, and so does the convention (a2). Convention (a1) is more in line with harmonic analysis.
into itself, and so does the convention (a2). Convention (a1) is more in line with harmonic analysis.
References
| [a1] | W. Rudin, "Functional analysis" , McGraw-Hill (1973) |
Fourier transform. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fourier_transform&oldid=44378