Anisotropic kernel
From Encyclopedia of Mathematics
The subgroup 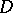 of a semi-simple algebraic group
of a semi-simple algebraic group 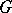 , defined over a field
, defined over a field 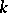 , which is the commutator subgroup of the centralizer of a maximal
, which is the commutator subgroup of the centralizer of a maximal 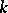 -split torus
-split torus 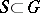 ;
; 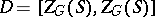 . The anisotropic kernel
. The anisotropic kernel 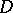 is a semi-simple anisotropic group defined over
is a semi-simple anisotropic group defined over 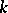 ;
; 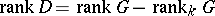 . The concept of the anisotropic kernel plays an important role in the study of the
. The concept of the anisotropic kernel plays an important role in the study of the 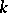 -structure of
-structure of 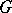 [1]. If
[1]. If 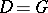 , i.e. if
, i.e. if 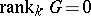 , then
, then 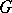 is anisotropic over
is anisotropic over 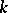 ; if
; if 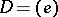 , the group
, the group 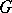 is called quasi-split over
is called quasi-split over 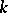 .
.
References
| [1] | J. Tits, "Classification of algebraic simple groups" , Algebraic Groups and Discontinuous Subgroups , Proc. Symp. Pure Math. , 9 , Amer. Math. Soc. (1966) pp. 33–62 |
| [2] | A. Borel, J. Tits, "Groupes réductifs" Publ. Math. IHES , 27 (1965) pp. 55–150 MR0207712 Zbl 0145.17402 |
How to Cite This Entry:
Anisotropic kernel. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Anisotropic_kernel&oldid=44271
Anisotropic kernel. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Anisotropic_kernel&oldid=44271
This article was adapted from an original article by V.P. Platonov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article