Homoclinic point

A point 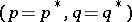which belongs to the domain of definition of the Hamilton function 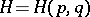of the Hamiltonian system

(*)

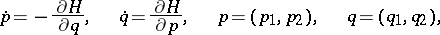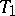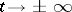and is such that the solution of the system (*) passing through it asymptotically approaches some periodic solution as . The solution passing through the homoclinic point is itself called homoclinic.

Let 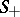be the surface formed by the solutions of (*) which asymptotically approach the periodic solution 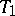as 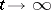, and let 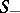be the surface formed by the solutions of (*) which asymptotically approach the same solution as 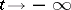. The set 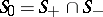will then consist of homoclinic solutions. If the surfaces 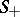and 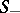intersect (or make a contact of odd order) along at least one homoclinic solution, then 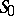will contain infinitely many different solutions. The case in which 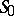contains a countable number of solutions is a structurally-stable case, i.e. 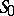is preserved if the function 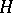changes by a small amount. The case in which 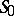contains an uncountable number of different solutions is not structurally stable, i.e. degenerate. It is assumed that the periodic solution 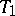itself and the surfaces and 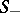are preserved if the function is changed by a small amount. This will be the case, for example, if the periodic solution 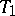is of hyperbolic type (cf. Hyperbolic point).

Finding homoclinic solutions of a system (*) with an arbitrary Hamilton function 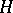is a difficult task. However, if it is possible to select the variables 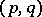so that the equation

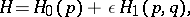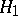where is a small parameter and the function is 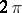-periodic with respect to the variable 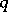, is valid, then the homoclinic solutions of (*) may be found in the form of convergent series (see reference [3] in Heteroclinic point). The existence of homoclinic solutions of (*) has been proved under much weakened restrictions on the Hamilton function of (*).

The above definition of a homoclinic point can be applied unaltered to the case of a Hamiltonian system with 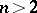degrees of freedom if the periodic solution 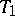is replaced by a 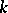-dimensional invariant torus 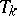, 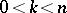. It is known that 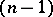-dimensional invariant tori have homoclinic solutions if they are of hyperbolic type.

A neighbourhood of a homoclinic solution has a complicated structure. For instance, it has been proved for the case of (*) that a countable number of periodic solutions with arbitrary large periods exists in a neighbourhood of a homoclinic solution, and that any two such solutions can be connected by a heteroclinic solution. Homoclinic solutions play an important role in the general theory of smooth dynamical systems.

See also the references to Heteroclinic point.

References

[1]	H. Poincaré, "Les méthodes nouvelles de la mécanique céleste" , 1–3 , Gauthier-Villars (1892–1899)
[2]	F. Takens, "Homoclinic points in conservative systems" Invent. Math. , 18 (1972) pp. 267–292
[3]	V.K. Mel'nikov, "On the existence of doubly asymptotic trajectories" Soviet Math. Dokl. , 14 : 4 (1973) pp. 1171–1175 Dokl. Akad. Nauk SSSR , 211 : 5 (1973) pp. 1053–1056
[4]	Z. Nitecki, "Differentiable dynamics. An introduction to the orbit structure of diffeomorphisms" , M.I.T. (1971)

Comments

The notion of a homoclinic point is not restricted to Hamiltonian dynamical systems. For a survey of recent developments see [a1].

References

[a1]	F. Takens, "Homoclinic bifurcations" A.M. Gleason (ed.) , Proc. Internat. Congress Mathematicians (Berkeley, 1986) , Amer. Math. Soc. (1987) pp. 1229–1236
[a2]	J. Guckenheimer, P. Holmes, "Non-linear oscillations, dynamical systems, and bifurcations of vector fields" , Springer (1983)