Homoclinic point
A point 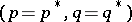 which belongs to the domain of definition of the Hamilton function
which belongs to the domain of definition of the Hamilton function 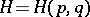 of the Hamiltonian system
of the Hamiltonian system
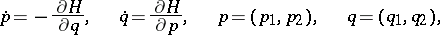 | (*) |
and is such that the solution of the system (*) passing through it asymptotically approaches some periodic solution 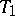 as
as 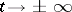 . The solution passing through the homoclinic point is itself called homoclinic.
. The solution passing through the homoclinic point is itself called homoclinic.
Let 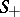 be the surface formed by the solutions of (*) which asymptotically approach the periodic solution
be the surface formed by the solutions of (*) which asymptotically approach the periodic solution 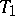 as
as 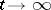 , and let
, and let 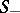 be the surface formed by the solutions of (*) which asymptotically approach the same solution as
be the surface formed by the solutions of (*) which asymptotically approach the same solution as 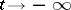 . The set
. The set 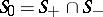 will then consist of homoclinic solutions. If the surfaces
will then consist of homoclinic solutions. If the surfaces 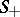 and
and 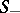 intersect (or make a contact of odd order) along at least one homoclinic solution, then
intersect (or make a contact of odd order) along at least one homoclinic solution, then 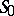 will contain infinitely many different solutions. The case in which
will contain infinitely many different solutions. The case in which 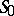 contains a countable number of solutions is a structurally-stable case, i.e.
contains a countable number of solutions is a structurally-stable case, i.e. 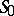 is preserved if the function
is preserved if the function 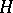 changes by a small amount. The case in which
changes by a small amount. The case in which 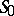 contains an uncountable number of different solutions is not structurally stable, i.e. degenerate. It is assumed that the periodic solution
contains an uncountable number of different solutions is not structurally stable, i.e. degenerate. It is assumed that the periodic solution 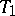 itself and the surfaces
itself and the surfaces  and
and 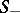 are preserved if the function
are preserved if the function  is changed by a small amount. This will be the case, for example, if the periodic solution
is changed by a small amount. This will be the case, for example, if the periodic solution 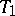 is of hyperbolic type (cf. Hyperbolic point).
is of hyperbolic type (cf. Hyperbolic point).
Finding homoclinic solutions of a system (*) with an arbitrary Hamilton function 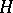 is a difficult task. However, if it is possible to select the variables
is a difficult task. However, if it is possible to select the variables 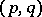 so that the equation
so that the equation
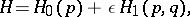 |
where  is a small parameter and the function
is a small parameter and the function 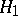 is
is 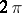 -periodic with respect to the variable
-periodic with respect to the variable 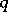 , is valid, then the homoclinic solutions of (*) may be found in the form of convergent series (see reference [3] in Heteroclinic point). The existence of homoclinic solutions of (*) has been proved under much weakened restrictions on the Hamilton function of (*).
, is valid, then the homoclinic solutions of (*) may be found in the form of convergent series (see reference [3] in Heteroclinic point). The existence of homoclinic solutions of (*) has been proved under much weakened restrictions on the Hamilton function of (*).
The above definition of a homoclinic point can be applied unaltered to the case of a Hamiltonian system with 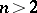 degrees of freedom if the periodic solution
degrees of freedom if the periodic solution 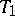 is replaced by a
is replaced by a 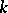 -dimensional invariant torus
-dimensional invariant torus 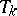 ,
, 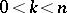 . It is known that
. It is known that 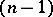 -dimensional invariant tori have homoclinic solutions if they are of hyperbolic type.
-dimensional invariant tori have homoclinic solutions if they are of hyperbolic type.
A neighbourhood of a homoclinic solution has a complicated structure. For instance, it has been proved for the case of (*) that a countable number of periodic solutions with arbitrary large periods exists in a neighbourhood of a homoclinic solution, and that any two such solutions can be connected by a heteroclinic solution. Homoclinic solutions play an important role in the general theory of smooth dynamical systems.
See also the references to Heteroclinic point.
References
| [1] | H. Poincaré, "Les méthodes nouvelles de la mécanique céleste" , 1–3 , Gauthier-Villars (1892–1899) |
| [2] | F. Takens, "Homoclinic points in conservative systems" Invent. Math. , 18 (1972) pp. 267–292 |
| [3] | V.K. Mel'nikov, "On the existence of doubly asymptotic trajectories" Soviet Math. Dokl. , 14 : 4 (1973) pp. 1171–1175 Dokl. Akad. Nauk SSSR , 211 : 5 (1973) pp. 1053–1056 |
| [4] | Z. Nitecki, "Differentiable dynamics. An introduction to the orbit structure of diffeomorphisms" , M.I.T. (1971) |
Comments
The notion of a homoclinic point is not restricted to Hamiltonian dynamical systems. For a survey of recent developments see [a1].
References
| [a1] | F. Takens, "Homoclinic bifurcations" A.M. Gleason (ed.) , Proc. Internat. Congress Mathematicians (Berkeley, 1986) , Amer. Math. Soc. (1987) pp. 1229–1236 |
| [a2] | J. Guckenheimer, P. Holmes, "Non-linear oscillations, dynamical systems, and bifurcations of vector fields" , Springer (1983) |
Homoclinic point. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Homoclinic_point&oldid=13448