Euler numbers
The coefficients 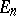 in the expansion
in the expansion
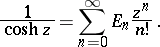 |
The recurrence formula for the Euler numbers (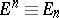 in symbolic notation) has the form
in symbolic notation) has the form
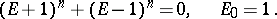 |
Thus, 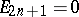 , the
, the 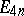 are positive and the
are positive and the 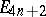 are negative integers for all
are negative integers for all 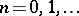 ;
;  ,
, 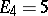 ,
, 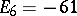 ,
, 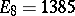 , and
, and  . The Euler numbers are connected with the Bernoulli numbers
. The Euler numbers are connected with the Bernoulli numbers 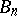 by the formulas
by the formulas
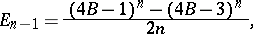 |
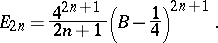 |
The Euler numbers are used in the summation of series. For example,
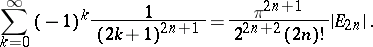 |
Sometimes the 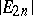 are called the Euler numbers.
are called the Euler numbers.
These numbers were introduced by L. Euler (1755).
References
| [1] | L. Euler, "Institutiones calculi differentialis" G. Kowalewski (ed.) , Opera Omnia Ser. 1; opera mat. , 10 , Teubner (1980) |
| [2] | I.S. Gradshtein, I.M. Ryzhik, "Table of integrals, series and products" , Acad. Press (1980) (Translated from Russian) |
Comments
The symbolic formula 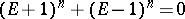 should be interpreted as follows: first expand the left-hand side as a sum of the powers
should be interpreted as follows: first expand the left-hand side as a sum of the powers 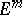 , then replace
, then replace 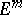 with
with 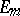 . Similarly for the formula connecting the Bernoulli and Euler numbers. The Euler numbers
. Similarly for the formula connecting the Bernoulli and Euler numbers. The Euler numbers 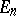 are obtained from the Euler polynomials
are obtained from the Euler polynomials 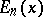 by
by 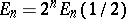 .
.
References
| [a1] | A. Segun, M. Abramowitz, "Handbook of mathematical functions" , Appl. Math. Ser. , 55 , Nat. Bur. Standards (1970) |
Euler numbers. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Euler_numbers&oldid=43465